A Finite Universe?

A Finite Universe? (May 27, 2004)

Introduction

Is our universe finite or infinite? It is not easy to understand this question, let alone answer it. However, researchers are analyzing new data which may help answer several fundamental questions about the nature of our universe.

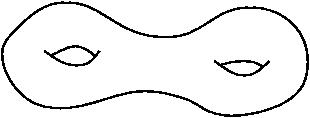
To get a handle on the meaning of this question, try performing the following thought experiment. Imagine that we don't yet know that the surface of the earth is a sphere. It may be quite difficult to determine its nature by investigating only a small area. Perhaps it seems to stretch on forever in all directions, and yet it is still possible that it curves around and meets up with itself and is finite. Even if we concluded that the surface of the earth was finite, we would still have to determine which finite surface it is. It could be a sphere, or a torus, or a surface with two 'holes':

or 10 holes, or 97. These surfaces don't have edges, and yet they are finite.

This thought experiment is a little misleading in some ways. Perhaps you were imagining a donut shaped earth out in space with some other planets and beyond that stars and black holes and such. However, it is possible that our universe is finite and there is nothing outside of it. The question of whether there is something outside of our universe is a completely different question and one which is most likely impossible to ever answer.

A few 3-manifolds

Let's investigate some possible shapes for our universe. A torus can be formed by gluing the sides of a square together:

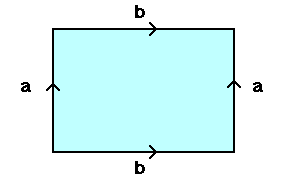
We can use this same idea to get 3-manifolds by gluing the faces of a cube. [A 3-manifold is a space which, at every point, there is a little region around the point which looks like a 3-dimensional ball.] If we glue the top to the bottom, the front to the back, and the left side to the right side, we get a 3-torus. Imagine standing inside the 3-torus.

When you look straight ahead, your line of sight continues through the front of the cube and into the back and you see the back of your head. There would be no trace of the faces of the original cube. You could start walking and walk right back to where you started without ever turning around.

There are other ways that one can glue the faces of a cube. One face can be glued to another with a twist or a flip. The MEC explored the possibilities which lead to possible shapes of our universe through some visualization exercises.

Three manifolds formed by identifying faces of a cube are just the tip of the iceberg. Understanding 3-manifolds is still an active area of mathematical research. However, even if we understood 3-manifolds very well, it would still be very difficult to figure out the shape of our universe. But, in recent years, researchers have been collecting and analyzing data to try and do just this.

The Cosmic Microwave Background

The cosmic microwave background consists of microwave radiation which permeates the entire universe. It is believed that it is the remnants of radiation emitted when the universe was formed and reflects a picture from about 300,000 years after the Big Bang.

The cosmic microwave background is extremely uniform. However, there are very small temperature fluctuations (on the order of millionths of a degree) which correspond to density fluctuations in the early universe. Accurate measurements of these temperature fluctuations could help determine the shape of our universe. In 2001, the Wilkinson Microwave Anisotropy Probe (WMAP) was launched to try and do just this. Researchers have compared the results with what would be expected for different models of the universe. As it turns out, the infinite universe model doesn't do very well with the part of the data which corresponds to wide-angle temperature fluctuations. However, there is a finite universe model which is a very good match for the data.

The Pioncaré dodecahedral space is formed by taking a dodecahedron and gluing pairs of opposite faces. To make the identification, we need to make a twist of pi/5 (pi is approximately 3.14). This would be a pretty interesting conclusion. However, the evidence is far from conclusive. In fact, there are researchers who feel that they have pretty good evidence that this model is not the correct one, and other researchers who have suggested other models.