Games as Trees

The 15 Game

To play the 15 game, write the numbers 1 through 9 in a square. Player one is X and player two is O. Player one starts by drawing an X through any unchosen number. Then player two circles an unchosen number. The game is won when one player has collected three numbers which add up to 15. In the sample game, player two has won because 8 + 6 + 1 = 15. Note that having 9 and 6 alone would not be a win even though 9 + 6 = 15, because you need three numbers which sum to 15.

Strategy

What is the best first move for player one?
Does one of the players have a forced win?
Are draws possible? Can either player force a draw?
Does this game feel familiar? Can you related it to some other game you already know?

Abstract Games

What does it mean for two games to be the same? Why is chess the same game whether you play with plastic pieces or ivory pieces? In what sense is the 15 Game the same as Tic-Tac-Toe? One way to approach these questions is to draw a game tree. A game tree is an abstract representation of an actual game. To draw a game tree, draw one dot to represent the starting position of the game. Now for each legal move that player one has, draw a new branch coming out of the dot. For example, X has nine possible moves at the start of a Tic-Tac-Toe game, so the initial dot will have nine edges coming out of it. The ends ("leaves") of these branches each represent a possible position that player two will see. Add new branches corresponding to the legal moves that player two has. Repeat this process, only stopping when you have reached a position representing the end of the game.

Part of the game tree for 2x2 Tic-Tac-Toe

Playing the Tree-climbing Game

A mathematical tree is a graph with no loops. One point of the graph should be singled out as the root of the tree.

To play the tree-climbing game, draw any tree. Player one starts at the root and climbs up a branch to any neighboring point. Then player two climbs to any neighbor of that point, and so forth (no backtracking allowed!). The first player to reach the treetop wins. Conversely, the first player who is stuck and cannot climb higher loses.

Suppose we draw the game tree for some game, such as Chess. In what sense is playing the tree-climbing game using this tree the same as playing Chess?
Every tree-climbing game has a winner or loser -- there are no ties possible. We can modify an existing game that has ties by declaring the first player who cannot make a legal move the loser. With this in mind, who wins the tree-climbing game for Tic-Tac-Toe given best play?
Sketch a few interesting parts of the game tree for Tic-Tac-Toe.
How many branches come out of the starting position in the game tree for Chess?

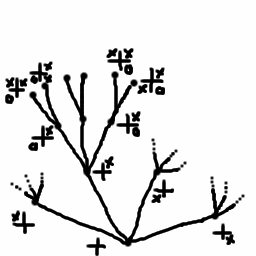
The Number Game

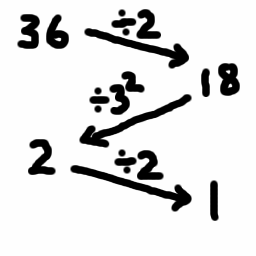
To play the number game, choose any positive whole number n as your starting position. To make a move, choose a prime p which divides n. Then divide n by whatever positive power of p that you like, as long as the result is still a whole number. For example if n = 12, the valid moves are 3, 2, and 4 (2²) resulting in the positions 4, 6, and 3 respectively. A player loses if n = 1 on the start of their turn, since this means they have no legal moves left.

What does the game tree for the number game look like starting at n = 12? What is the best strategy for the first player? Who wins the game?
Play the number game using different values of n. Which games are a win for the second player? Draw the game trees for some of these games and work out the best strategies.

Finding the Winner of Any Game

Since the game tree knows everything about how a game is played, we can use it to predict who the winner is. To do this, we will use a recursive algorithm. First, let us define some terminology relating to trees. For a point on the tree, the edges rising out of the point are called branches. In a game tree, the branches represent the possible moves that a player has in the given position. A point on a tree is a leaf if it does not have any branches coming out of it -- for game trees, the leafs are the same as the ending positions of the game. Given a point on the tree, the corresponding subtree is the part of the tree which rises out of that point.

Here is a recursive process for creating an algebraic expression involving x from a tree:

Start at the root of the tree.
Write an x for each branch coming out of your current location in the tree. If there are no branches, write 1 instead and skip the next step.
Now we must figure out what to write in the exponent of each x that we wrote. To do this, look at the subtree starting at the end of each branch and repeat these steps for that subtree.

This is a little tricky to understand in writing, but easier to understand by example. Study the two diagrams below until you understand how to use this recursive algorithm.

To check that you understand the algorithm, try to turn the game tree for the number game starting at n = 12 into an expression. You should get the following answer:

To find out who the winner is, set x = 0 and simplify, using the rules

1¹ = 1
1⁰ = 1
0¹ = 0
0⁰ = 1

If you get zero, then the first player has a winning strategy. If you get one, then the second player has a winning strategy. This means that you can figure out who wins any game just by finding the game tree, converting it to an expression and simplifying the result when x = 0!

Use this method on some of the game trees you have worked out to see who the winner is under optimal play.
We can define the product of games A and B as follows: player one chooses either A or B, then player two makes the first move in that game. Then play continues as usual. If A and B correspond to the game tree expressions a and b, show that the game tree expression for the product of A and B is a b. (hint: what does the game tree look like for the product of A and B?)
We can also define the exponential of A and B: player one plays the first move of game A. Then player two can choose to either continue playing game A, or switch to game B and make the first move. Show that the game tree expression for the exponential is a^b.
Do the rules A^CB^C = (AB)^C and (A^B)^C = A^BC hold for games?