Birthday Problem

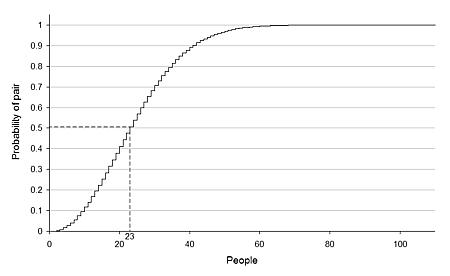
As an application of the Poisson approximation to Binomial, we consider the Birthday problem, which is quite interesting. Do you know whether there are two students in your class having the same birthday? (This question is different from is there any student in your class who has the same birthday as you.) The answer in probability is quite surprising: in a group of at least 23 randomly chosen people, the probability that some pair of them having the same birthday is more than 50%. For 57 or more people, the probability reaches more than 99%. And of course, the probability reaches 100% if there are 367 or more people. Below is a graph showing the probability against size of the group.

In computing the probability p(n) that in a room of n people, there exists at least a pair that has the same birthday, we ignore the variation in distribution (in reality, not all the dates are equally likely) and assume the distribution of birthdays are uniform around a year of 365 days.It is easier first to calculate the probability that all n birthdays are different. Of course, if n is larger than 365, by the pigeonhole priciple, there must be two birthdays on the same day, so the probability is 0. When n is less or equal to 365, we have

Below is the graph of probabililty of no match against n:

The event that at least one pair has the same birthday is complementary to the event that all n birthdays are different. Therefore p(n) is equal to 1 minus the above probability.

To carry out effective approximation when n is large, we need the following lemma:

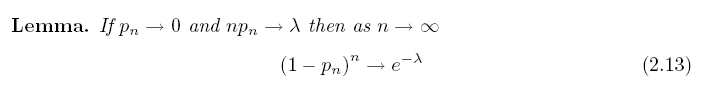
Therefore

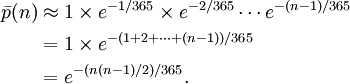
You can plug in n=23 and n=57 to the above formula to check if the previous statement is correct.

What about the assumption that birthdays are uniformly distributed? In reality, birthdays are not uniformly distributed.

In particular, many children are born in the summer, especially the months of August and September (for the northern hemisphere), and in the U.S. it has been noted that many children are conceived around the holidays of Christmas and New Year's Day; and, in environments like classrooms where many people share a birth year, it becomes relevant that due to the way hospitals work, where C-sections and induced labor are not generally scheduled on the weekend, more children are born on Mondays and Tuesdays than on weekends. Both of these factors tend to increase the chance of identical birth dates, since a denser subset has more possible pairs (in the extreme case when everyone was born on three days, there would obviously be many identical birthdays). The birthday problem for such non-constant birthday probabilities was tackled by Murray Klamkin in 1967. A formal proof that the probability of two matching birthdays is least for a uniform distribution of birthdays was given by D. Bloom (1973)

The answer is that the probability of a match onlly becomes larger for any deviation from the uniform distribution. This result can be proved rigorously but involves more mathematics. Intuitively, you might better understand the result by thinking of a group of people coming from a planet on which people are always born on the same day! Then actually 100% any pair is a match, of course, this is the greatest deviation from the uniform distribution I can think of.