
return to the Geometric Dissections menu
Hinged Dissections
Hinged dissections are dissections with a chain-like property: we can disassemble an original figure in such a way that all the pieces are linked at least at one point, and a new rearrangement is possible by continuously moving of the pieces, without destroying the chain.
According to Frederickson, who published in 2002 the most remarkable book on this subject,[1] the idea of hinged dissections originated in early twentieth century with Henry Ernest Dudeney. Famously, Dudeney also gave a hingeable dissection of the equilateral triangle to a square:[2]

Not all dissections are hingeable dissections, so hingeable dissections are a special class of dissections. Yet the hingeable condition leaves room for a multitude of possible problems in hingeable dissections. I exemplify with a succession of hingeable dissections taken from Greg Frederickson’s 2002 book.
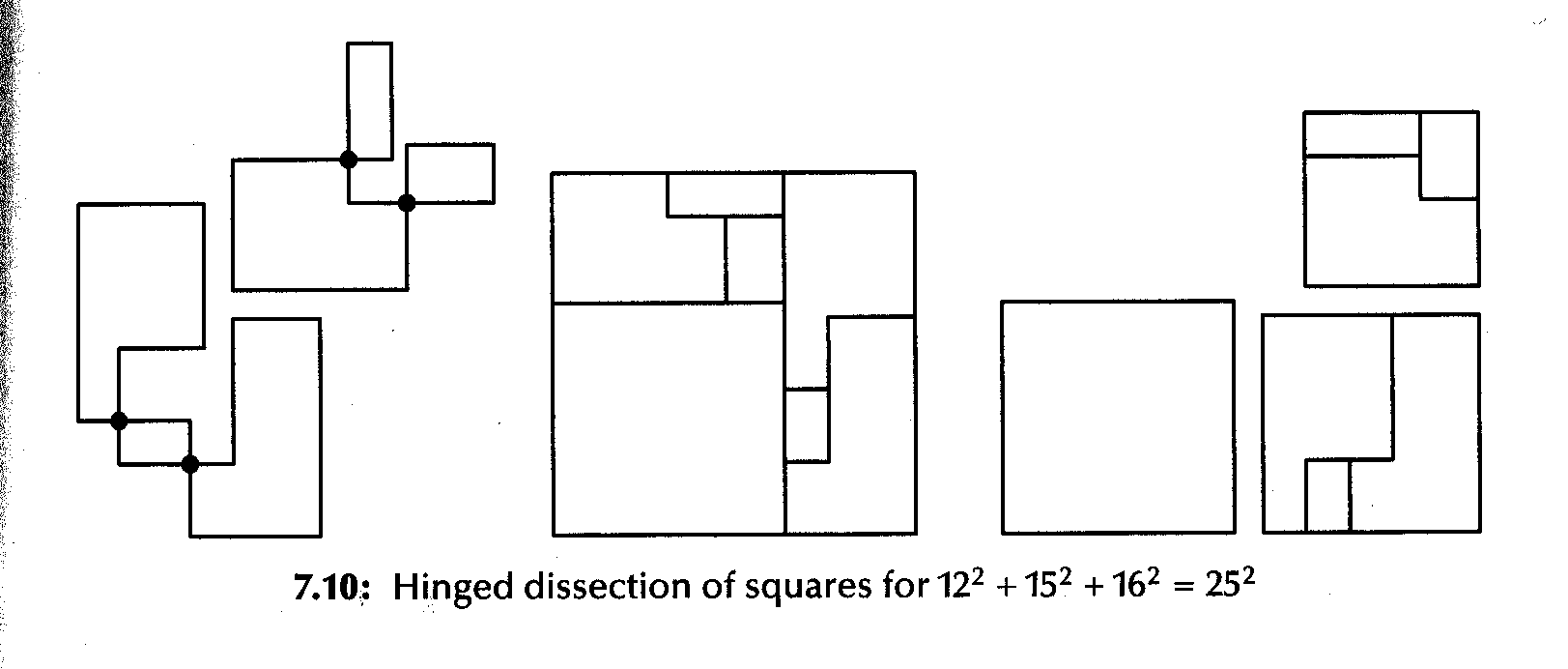
Let’s start with a simple hingeable dissection of two unequal squares to one square:
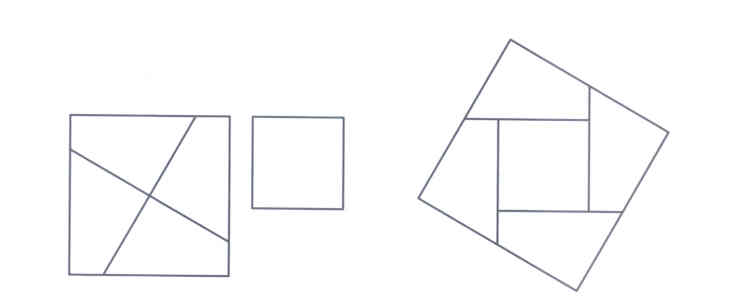
There are many variations on this theme. Here are a few others, for triangles,
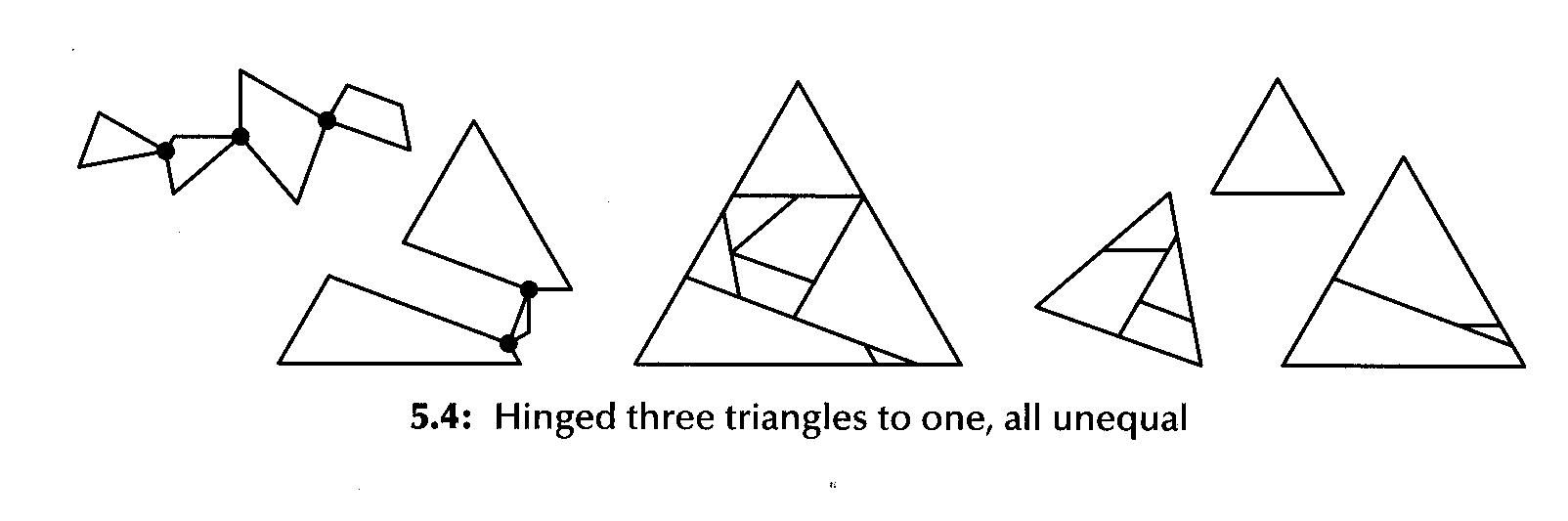
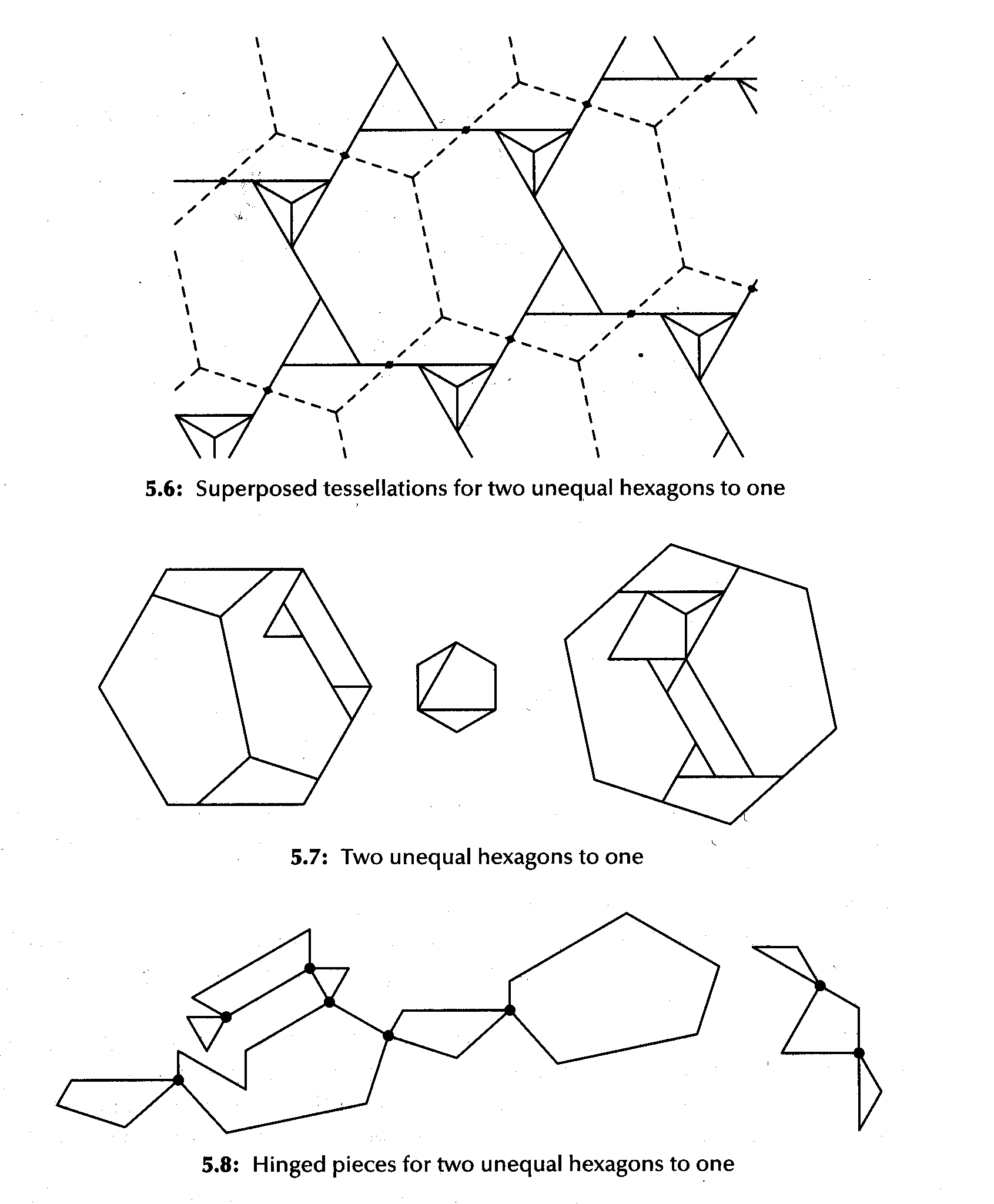
for hexagons,
for pentagons,

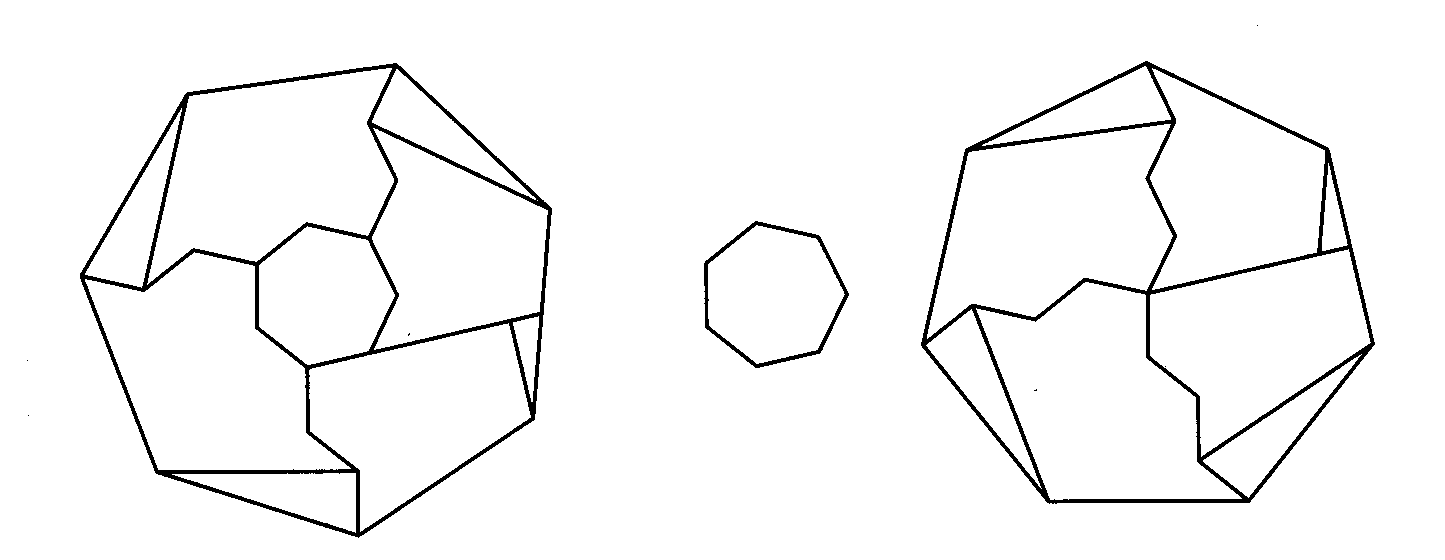
for heptagons,
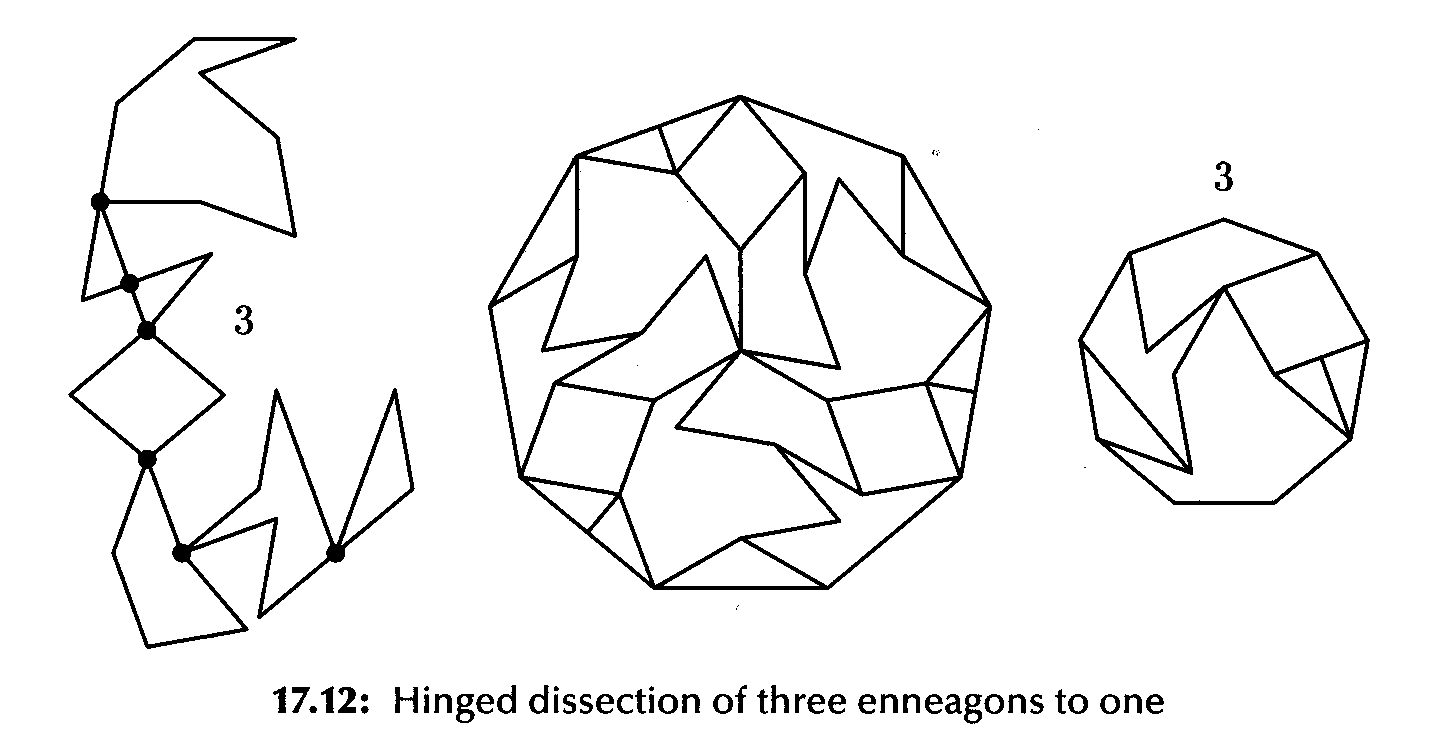
for enneagons,
for dodecagons,

for a different combination of squares:
for hingeable dissections of a dodecagon to a square,
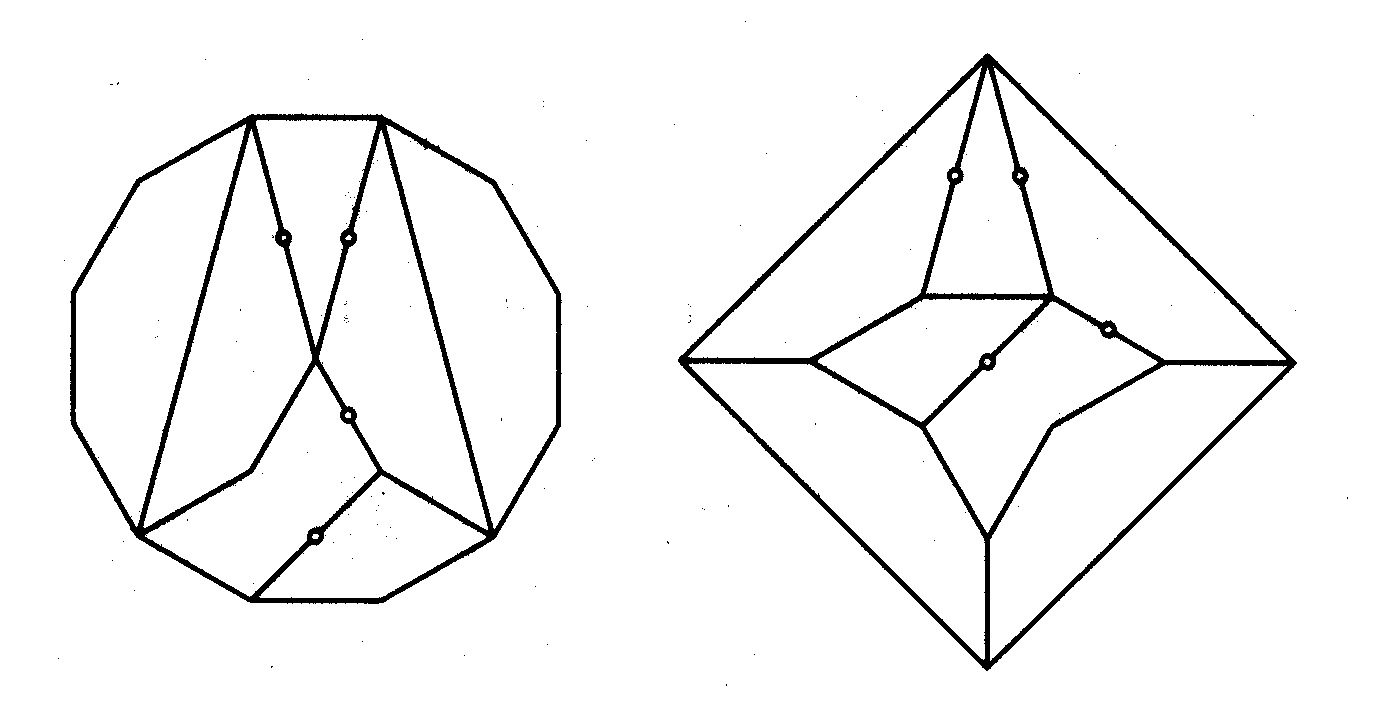
as well as one of a dodecagon to three equal squares:
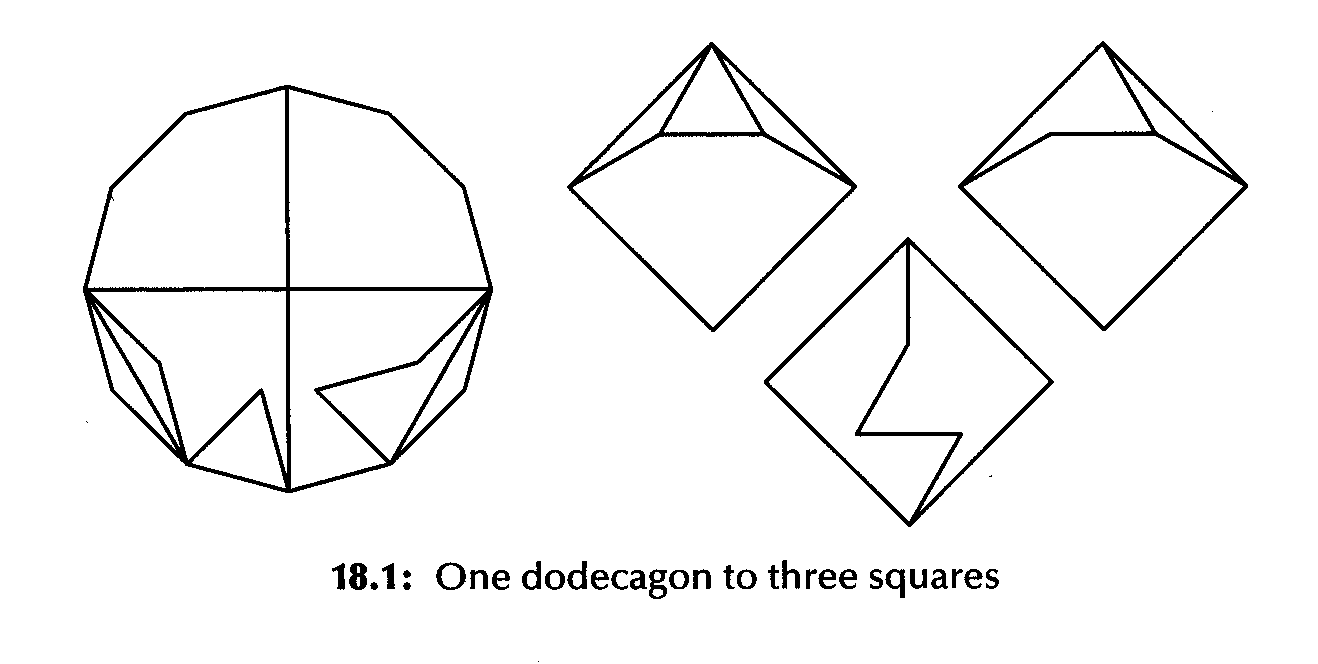
We conclude with the detailed figures of the cross-strips that produce a hingeable dissection of a pentagon to a triangle
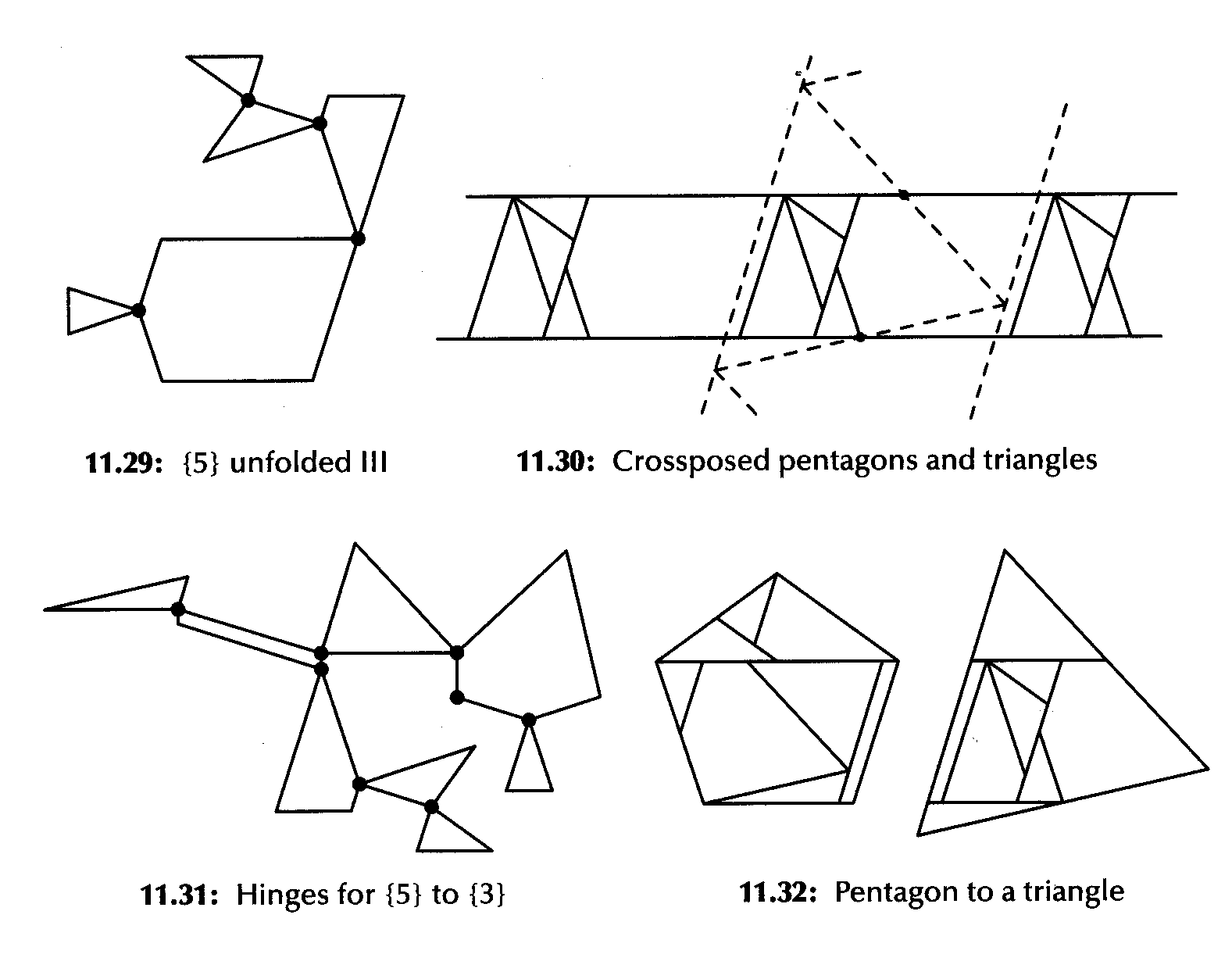
and a haxagram to a hexagon:

For still open questions in hinged geometrical dissections, see the article by David Eppstein mentioned in the Resource subsection.
ENDNOTES:
[1] Frederickson 2002, p. 1.