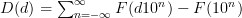Scale-Invariance

To give a definition of scale-invariance, we start with a sequence $latex \{a_n\}$. To simplify notations, let D(d+1) denote the probability that a number from the sequence has leading digit at most d, and F(x) denotes the probability that a number from the sequence is less than x (aka cumulative distribution function). So

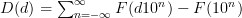______ (eq 1)

After we change the unit, 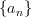becomes , and denote the new D and F with a bar on top, so , and scale invariance means . Repeatedly using eq 1,

Summarizing,

D(c d) = D(c)+ D(d)}, for d=2, ..., 10, and c>0 ______ (eq. 2)

D(d) = log d satisfies eq. 2, but does eq. 2 implies D(d) = log d (for d=2, ..., 10)?

First, we need to assume D(10)=1, which is reasonable. Second, we extend D to accept positive real numbers as input, not just positive integers, so that we can talk about D being continuous, which we will also assume (This is still reasonable if we take eq. 1 as the definition of D.). Then the answer is yes.

Exercise: D(1)=?

Answer: Let c=1, then D(1)=1 by eq. 2.

Exercise: Using D(1) and D(10), can you figure out other values of D using eq. 2?

For example, D(1/10)=-D(10)=-1 or more generally $latex D(10^n)=n$. That's about it without being clever.

Trick for D(2): we only need to figure out D(2^q) for some integer q, because D(2^q)=q D(2). The only thing we know is D(10^p)=p, so try to find integers q and p so that

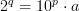________ (eq. 3)

where a is close to 1 (impossible for a to be 1, why?). After taking log, this means we want to approximate latex log 2 by p/q such that q log 2 is as close to an integer as we want, which is possible by Lemma 1 as log 2 is irrational. Finally applying D to eq. 3 (and simplifying using eq. 2 many times) gives

q D(2)=p+D(log a)

, and in the limit as a approaches 1, p/q approaches log 2 and D(a) approaches 0 by continuity of D , so D(2)= log 2. Similar arguments give

D(d)=log d

where d>0.

Next: base-invariance or if you are tired, go Home