Copy the below 9x9 grid and complete it so that each row, each column, and each 3x3 box with a thick margin contains each of the numbers 1 to 9 exactly once.

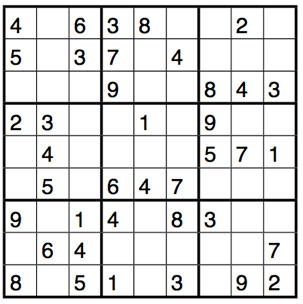
Since you are reading an article on the Mathematics of Sudoku puzzles, this is probably an easy exercise for you already. On this webpage, we will not focus on how to solve the New York Times puzzle faster than the person sitting next to you (although we will learn some advanced solving tricks), but on aspects of Sudoku that are interesting from a mathematical perspective. By a Sudoku puzzle, we will mean a puzzle on a 9x9 grid like the one above, unless something different is stated explicitly.

You might wonder how many possible different 9x9 grids there are. What about N2 x N2 grids for any positive number N? And when will the New York Times run out of Sudoku puzzles ? We will count Sudoku puzzles in section 1. Just like a Sudoku solver presented with a particularly hard puzzle, a Mathematician will be interested in when puzzles have unique solutions. Section 2 is the beginning of a discussion on the existence and uniqueness of solutions to Sudoku puzzles. In sections 3 and 4, we look at solving algorithms for Sudoku puzzles. One of them will be relatively straightforward in theory, but impossible to use without a computer, while the other is more complicated, but enables a human being to solve any Sudoku puzzle that has a solution at all. Section 5 explains how Sudoku puzzles are related to graphs, and why this connection is so useful.

I encourage you to attempt the activities that you can find throughout the sections. You can find outlines of solutions in section 6, and some sources of further information in section 7.

What do you get out of all of this? A totally new way of looking at Sudoku puzzles,  the right to claim that there is no Sudoku puzzle you can’t beat, and, unless you have taken university-level Math or Computer Science classes before, mastery of some mathematical concepts for which you will find applications again and again in your life. Have fun!