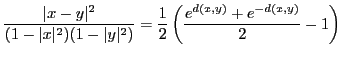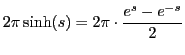|
7. The Poincaré disk model for the hyperbolic planeThe second model that we use to represent the hyperbolic plane is called the Poincaré disk model, named after the great French mathematician, Henri Poincaré (1854 - 1912). This model is constructed starting from the previous one. You may ask yourself why is it necessary to do that? The reason is that this model is more useful, as it gives more insight and we can make a better use of the apparatus from the complex analysis. As you will see at the end of this page, it is this model that appears in Escher's work.
Hyperbolic Lines
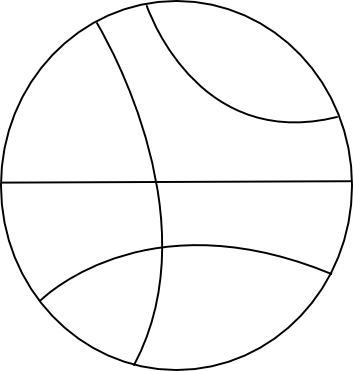
Remember that in the half-plane case, the lines were either Euclidean lines, perpendicular onto the real line, or half-circles, also perpendicular onto the real line. In the Poincaré case, lines are given by diameters of the circle or arcs. Here is a figure to give you an idea:
Distances in hyperbolic plane
Property 1
For each pair
where
This tells us that it's pretty complicated to calculate the hyperbolic distance in
Hyperbolic circles
Definition 1
A hyperbolic circle in
where
We can completely characterise hyperbolic circles in
Property 2
A hyperbolic circle in
Property 3
Given
(Remember, in the Euclidean the circumference is
Note that any hyperbolic circle is inside the Poincaré disk, so from the Euclidean point of view any circle here has radius less than
Exercise 1
Let
Exercise 2
Let
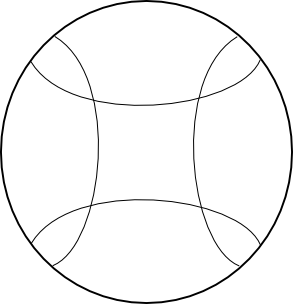
Hyperbolic polygons
Definition 2
A hyperbolic polygon is a closed convex set in the hyperbolic plane, that can be expressed as the intersection of a (locally finite) collection of closed half-planes.
(What locally finite means is a bit complicated to explain, it requires some deep analysis. But in principle it means that if we would enlarge (with a good enough microscope) the intersections between neighbouring half-planes, there will always be finitely many planes which intersect).
Hyperbolic fish and other beings...Like we said before, the Poincaré disk model is very good to visualise objects. Thanks to Escher we can see how "beings" (which are in fact more complicated 2-D objects) look in the hyperbolic plane. Here is again "Circle Limit III" and this time with its original sketch.
Although the fish appear smaller the closer you get to the boundary of the disk, they are the same size in the geometry of the hyperbolic plane. Similarly, all the white segments going from the fishes' tails to their noses are the same length (and they are, in fact, straight lines). This tells us that, in a way, we can imagine this plane as a kind of sphere, that has a point at infinity. "Circle Limit III" is not just a representation of the Poncaré disk in a more artistic way, it is also a tessellation of the hyperbolic. Tessellations were Escher's favourite game! Let's see what they are! |