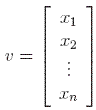
Lecture #1: Linear Algebra - in a Nutshell

We begin by setting up various pieces of background material related to linear algebra. The theory here is of course not explained in the most generality, but simplified and adapted to our discussion. Denote first the set of all real numbers by R. A vector of length n is simply a list of n elements, called vector entries. The notation of a (column) vector v having entries x1, x2, … ,xn is the following:

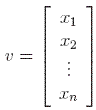
Example 1: The entries of a vector can in principle be anything: words, colors, numbers, etc. The following are all examples of vectors:

However, we will only look at vectors whose entries are real numbers (that is x1, x2, … ,xn are all real numbers). As in the case of real numbers, real vectors can be added or multiplied by a real number (called scalar) in a straightforward way:

Example 2: Under the above two notation we can easily check that:

Problem #1:
  1. Is it possible to multiply two vectors? How about adding vectors of different lengths?
  2. How many vectors of length 5 with integer entries are there? What if we require that all entries be different?

In a similar way we define the notion of a matrix. An m × n matrix is a rectangular array of entries having hight m and width n. This can also be seen as stacking n vectors of length m one next to the other. Again, take the entries to be real numbers. We denote an m × n matrix A with entries aij by:

This means that on row i and column j we find the real number aij. For example, on the first row, second column lies element a12. Notice that a vector of length m is just a m × 1 matrix and a real number is a 1 × 1 matrix. If m = n then the matrix is called a square matrix, of size n. This is what we will consider from now on. It makes sense now to talk about the diagonal of a matrix, which consists of those elements for which the row number equals the column number ( the elements a11, a22, up to ann).

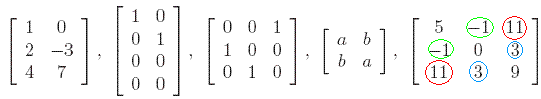
Example 3: The following are all examples of matrices, but only the last three are square:

Notice that the last two matrices are rather "special": they are symmetric. This means that entry on row i and column j is equal to that entry on row j and column i (or otherwise said aij = aji). As an easy exercise, prove that any diagonal matrix (has zeros everywhere, except on the diagonal) is symmetric. The matrix that has ones on the diagonal and zeros everywhere else is called the identity matrix and is denoted by I. Matrix multiplication is done in the following general way:

where the element cij is given by the formula:

Multiplying a matrix with a vector is done as follows:

where every element yi from the resulting vector y is given by the formula

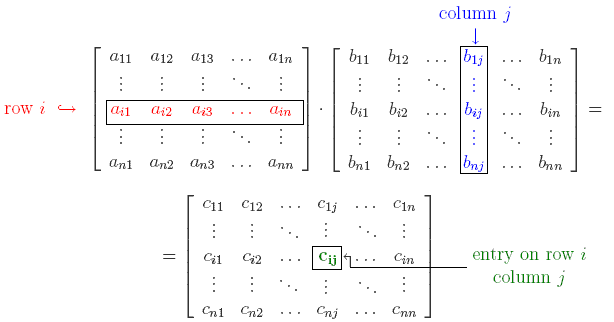
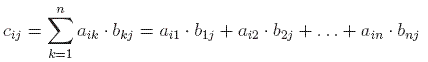
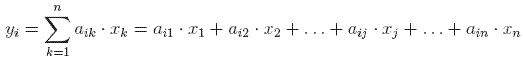
The other two matrix operations, addition and scalar multiplication, are done as in the case of vectors. Adding matrices A and B gives a matrix C which has the entry on row i and column j equal to the sum of the corresponding entries of A and B. Multiplying matrix A with a real number a is the same as multiplying every element of A with a.

Example 4: All above operations on matrices will become more obvious through the following examples:

Problem #2: Consider the following three matrices:

  1. What is the value of A+B, B·C, and A·B?
  2. Show that (A+B)+C = A+(B+C) and that (A·B)·C=A·(B·C).
  3. Find the product of A with the first column of C.
Fact 1: For any matrices A, B, C of the same size: (A+B)·C = A·C+B·C, and C·(A+B) = C·A+C·B.

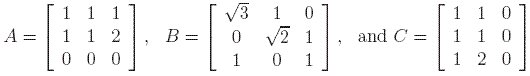
One can observe that there is some sort of similarity between matrices A and C in Problem 2. above. The similarity comes from the fact that the entry on row i and column j in matrix A is equal to the entry on row j and column i in matrix C. Of course, the elements on the diagonal are the same. We then say that A is the transpose of C, or equivalently that C is the transpose of A. In general, for a matrix A we denote its transpose by At. More intuitively, given a matrix we find its transpose by interchanging the element at row i, column j with the element at row j, column i. If we do this twice we notice that the transpose of the transpose of a matrix is the matrix itself, or (At)t=A.

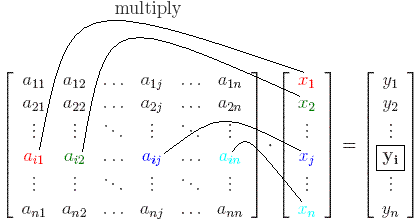
Fact 2: For any matrices A, B, (A·B)t = Bt·At, and (A+B)t = At+Bt.

We now introduce two important notions in the theory about matrices: eigenvector and eigenvalue. We say that the real number z is an eigenvalue for A if there exists a real vector v of length n such that A·v = z·v. Such a vector v is called an eigenvector corresponding to the eigenvalue z. This is not the most general definition, but it will suffice for our purposes. In general eigenvalues and eigenvectors are complex, and not real. If we assume that A is a (real) symmetric matrix of size n, then we know that it has n real eigenvalues and all eigenvectors are also real. In fact, a matrix of size n can have at most n real eigenvalues.

In order to make these definitions more clear, consider the following explicit example:

Example 5: The matrix has eigenvector 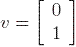and eigenvalue z = 3 corresponding to this eigenvector. Indeed, the definition is verified because:

Fact 3: Any matrix A has the same eigenvalues as its transpose At.

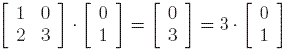
Of course, in general a matrix A and its transpose At do not have the same eigenvectors that correspond to the common eigenvalues. For the matrix in the above example, 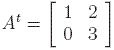has eigenvalue z = 3 but the corresponding eigenvector is 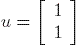. This follows from the computation below

An important observation is that a matrix A may (in most cases) have more than one eigenvector corresponding to an eigenvalue. These eigenvectors that correspond to the same eigenvalue may have no relation to one another. They can however be related, as for example if one is a scalar multiple of another. More precisely, in the last example, the vector whose entries are 0 and 1 is an eigenvector, but also the vector whose entries are 0 and 2 is an eigenvector. It is a good exercise to check this by direct computation as shown in Example 5.

A matrix is called column-stochastic if all of its entries are greater or equal to zero (nonnegative) and the sum of the entries in each column is equal to 1. If all entries of a matrix are nonnegative, then we say that the matrix itself is nonnegative. Furthermore, a matrix is positive is all its entries are positive (greater than zero) real numbers.

Example 6: Consider a matrix A with transpose At:

It is easy to see that A is column-stochastic, while At is not. However, the sum of the elements on each row of At is equal to 1. We first show that z = 1 is an eigenvalue for At, with corresponding eigenvector

This is true since At·v = 1·v. Then, from Fact 3, 1 is an eigenvalue for the matrix A as well.
Next we wish to find an eigenvector that corresponds to this eigenvalue for A. Let u be such an eigenvector. In order to find u explicitly we write the equation

x1, x2, x3, and x4 are all real numbers that we don't yet know. If we multiply term by term we find that

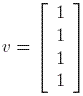
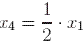Substituting in the third relation we obtain 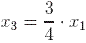and so the vector u is of the form

As x1 is just a real number (hence a scalar) we can take x1 = 12 and we have just proved that the vector whose entries are 12, 4, 9, and 6 (from top to bottom) is an eigenvector for A.

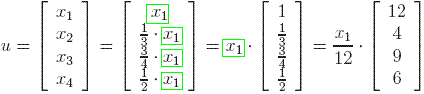
In the first part of the previous example we have just shown 1 is an eigenvalue for that particular case. However, this is true for any column-stochastic matrix, as stated below.

Fact 4: Any column-stochastic matrix has z = 1 as eigenvalue.

Notice also that the eigenvector that we found in the second part of the example above is rather "special" itself. We have chosen x1 = 12 and we obtained an eigenvector with positive entries. If however we choose x1 = -12 then we obtain an eigenvector with negative entries (smaller than 0).

Fact 5: If A is a positive column-stochastic matrix, then any eigenvector corresponding to the eigenvalue z = 1 has either only positive entries or only negative entries.
Problem #3: Show that the matrix is column stochastic and has z = 1 as eigenvalue. Find an eigenvector corresponding to this eigenvalue such that all its entries are positive.

When we are working with positive column-stochastic matrices A it is possible to find an eigenvector v associated to the eigenvalue z = 1 such that all its entries are positive. Hence A·v = v and the entries of v are all positive.

Fact 6: If A is a positive column-stochastic matrix, then there is a unique eigenvector corresponding to the eigenvalue z = 1 such that it has only positive entries the sum of its entries equals 1.

Back