Suppose you want to throw a party, and in order to make it interesting you want there to be at least three mutual friends or at least three mutual strangers present. How many people do you need to invite for this to happen? It turns out that the answer is surprisingly small, and holds intimations of much more difficult problems.
The complete graph on n vertices, Kn, is one where every vertex is connected by a single edge to each other vertex. Complete graphs are as connected as possible without containing duplicate edges, and so are frequently objects of study. They are also important in the social sciences where they are frequently called cliques.
Finding three mutual friends or three mutual strangers is thus a problem of finding a graph containing K3 as a subgraph, but what kind of graph are we looking for? One way to think about this is to imagine that we have two types of edges in our graph: one represents the "friend" relation, and one represents the "stranger" relation. Thus we are going to be considering colorings of complete graphs with two colors. The copies of K3 we will be looking for are monochromatic: all 3 edges share the same color.
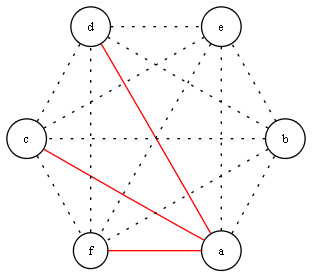
Let's consider what happens when we color K6. Take any vertex. This vertex has 5 edges, and while we may not know exactly how they are colored, we can tell that at least 3 of these edges will be of the same color, say red. Thus we have something resembling:

Next we consider what happens between the vertices at the end of these red edges. They can't be connected via red edges as this would give us a red copy of K3. Pick 2 of these edges and color them blue. Now we have something resembling:

Now we need to color the edge corresponding to the green one below:

However, we can't do this without making a monochromatic copy of K3. Don't be misled by the specificity of the pictures. The entire argument we have just gone through does not depend at all on which edges or vertices we consider; it is entirely determined by the use of 2 colors and the structure of K6. We can now see that inviting six people is sufficient to guarantee at least three mutual friends or at least three mutual strangers.
An important lesson to take away from the above argument is that it only shows that having 6 or more people in attendance allows for at least three mutual friends or three mutual strangers. Showing that not all parties with less than six people have this property is also necessary, which is the point of Activity 2.
Those who are not faint of heart might ask how large a party one might need in order to have 4 mutual friends or 4 mutual strangers, or even n mutual friends and n mutual strangers. These numbers are called the Ramsey numbers, R(n,n). One isn't limited to having the same size cliques for friends and strangers, and we might be interested in numbers like R(n,m).
A similar technique to the one used above allows us to calculate that R(4,3)=9, and using that we can bootstrap our way to finding that R(4,4)=18. In general, the Ramsey numbers are easier to find when n and m are not equal (mainly because one of n and m can be small), and it is often possible to provide upper and lower bounds for R(n,m) without finding the exact value. However, finding the exact value can be a Herculean task. To give you an idea of just how bad things get we leave with a quote from the mathematician Paul Erdos: