Numb3rs 408: Tabu

In this episode, Charlie uses a tabu search to predict the actions of a group that seems to have kidnapped a billionaire's daughter. A tabu search is a kind of local search: one moves from point to nearby point, trying to find an optimal solution.

Wandering in a fog

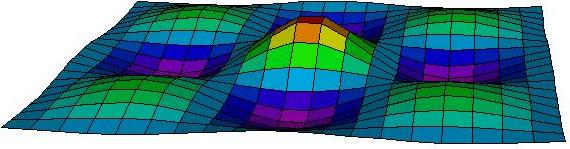
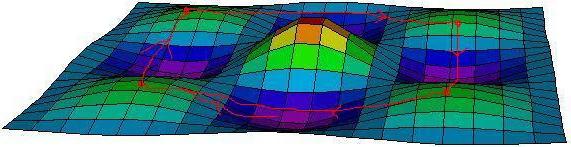
Suppose you are climbing a hilly terrain in a deep fog. We will call this terrain a search space. You can only see the area immediately around you, but you have a device for measuring your elevation. How do you find the highest point in the terrain? terrain
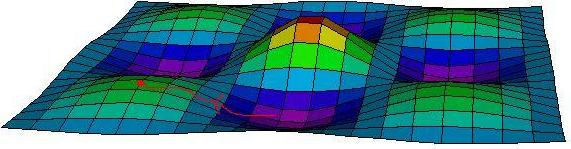
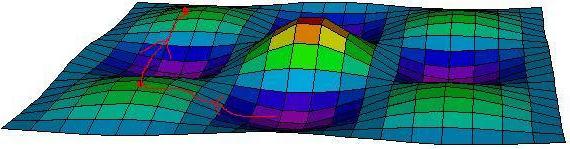
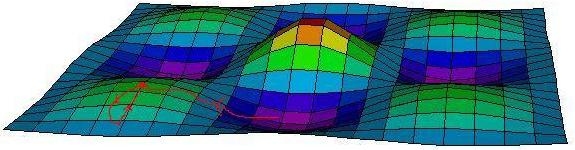
Your first thought might be to climb upwards, always walking towards the highest point you can see around you: this is an example of a greedy algorithm. Eventually you will reach the top of a hill. towards a hilltop
This hilltop, however, might not be the highest point in the terrain. To look for higher points, you will have to start walking downhill for a while. Eventually, you will want to start your uphill approach again. second hilltop
If you do this too soon, you will end up back at the same hilltop. towards a hilltop
When you reach a new hilltop, you can measure its height and compare it to the largest hill you have visited so far. You may end up walking around in circles, and never find the highest hills. walking in circles

Tabu Search

Tabu search, introduced by Fred Glover in 1986, addresses these issues by keeping track of your recent movement, avoiding course reversals. The idea is to make a tabu list of the recent types of moves you made in the search space, and prohibit reversing these moves for a period of time. For instance, if you move North, there is a period of time during which you may not move South, even if you first travel, say, East for a short time. Old tabus drop off the list as they are replaced by newer ones, so you may eventually be allowed to travel South. The fog wandering problem we just considered involves two degrees of freedom (North/South position and East/West position). A more realistic application of tabu search involves many variables. For instance, the diagram below illustrates a cycle of moves that could be prevented by a tabu list that contains three distinct prohibitions, but that would not be stopped by a shorter tabu list.

path on a cube Charlie describes a tabu search as "basically a way of excluding bad data - places where the kidnappers won't go to isolate where they will go." Actually, the main purpose of excluding choices in a tabu search is to prevent cycling. While tabu search can be applied to problems like the Travelling Salesman Problem where the goal is indeed to produce a path, it is important to distinguish between the path the algorithm follows in the search space and the elements of that search space (which happen to be paths). The tabus in our list impact our path through the search space; they do not remove particular paths from the search space. A particular implementation of tabu search can pragmatically prevent exploring particular areas of the search space where good solutions are unlikely to be found, but the main purpose of excluding choices in a tabu search is to prevent cycling.

Here is an outline of the basic tabu search heuristic. First the notation:

Here is the algorithm:

  1. Start at a random point p of the search space, or at a point that might be near a good solution. Set q=p and P=p.
  2. Let N denote the set of points of X that can be reached from q by a single move in M that is not in the tabu list L.
  3. Compute the value of each element of N under f.
  4. Change q to be the point with the largest value in the previous step.
  5. Add the reverse of the move just taken to the top of the tabu list L. If the tabu list is longer than T, remove the last entry from L.
  6. If f(q) > f(P), change P to q: we have found a new best solution.
  7. Return to step 2.

Modifications can be made to the above algorithm, such as allowing variable tabu list lengths, replacing N with a subset to reduce computation time, or adding aspiration criteria that allow tabus to be overriden on occasion. For instance, we may allow moves prevented by the tabu list if they lead to points in X where f has a larger value than f(P), the current best solution.

Travelling Salesman Problem without a computer

5 cities Choose 5 cities, and look up the cost for travelling between them (or make them up). Assume the cost is the same in both directions, so that you have 10 different costs, represented by the edges of the graph to the right. The Travelling Salesman Problem is to find the Hamiltonian Cycle (round trip path visiting each city exactly once) of minimal cost. There are only 12 different paths, so it is feasible to compute the cheapest cost, but let's try to use this problem to illustrate a tabu search.

In the tabu algorithm presented above, X is the set of Hamiltonian cycles. The function f applied to a cycle is the total cost of the route times -1 (so that maximizing f corresponds to minimizing the cost. Alternatively, replace "largest" with "smallest" and ">" with "<" in the algorithm.) Choose a value for T.

For the move set M, let's use moves of the form "swap the order in which we visit Ithaca and NYC given that these cities consecutively in the cycle". Such a move is its own inverse. For a given cycle, there are 5 moves that can apply. Now, apply the tabu search. Do you find the best solution before cycling occurs?

Computer programming

If you are familiar with computer programming, try implementing the above algorithm for a larger number of cities. Compare the results of this algorithm to those of a brute force algorithm running for the same amount of time. Experiment with length of the tabu list. Does cycling occur?

Try changing the move tabus as follows:

What effect if any do these changes have on algorithm performance?
Terrain images on this page were generated using JavaView.