In the episode Obsession, a photographer is killed while attempting to take tabloid sex photos. In an effort to retrace the photographers steps, the FBI examine his camera. They find a series of photos of a basketball hoop, each showing the hoop's shadow. Since each photograph is timestamped, Charlie was able to use the behavior of the hoop's shadow to pinpoint the longitude and latitude where the photos had been taken.
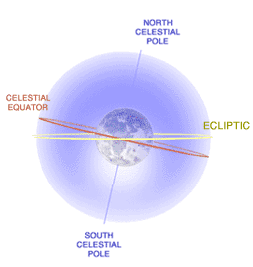
In order to make calculations involving the position of the sun in the sky, Charlie used a technique called spherical astronomy. In this subject, all observable planetary bodies and stars are assumed to lie on the celestial sphere, an imaginary rotating sphere of gigantic radius concentric to the Earth. In ancient Greece, this model was believed to be an accurate representation of the universe. Although we now know that these observed rotations are actually caused by the rotation of the earth itself rather than some super-sphere, scientists still use the techniques of spherical astronomy, which are often quite accurate and simplify calculations a great deal.
Spherical astronomy works particularly well for calculations involving constellations and other far away objects, as their movement is barely perceptible from Earth (the movement of stationary bodies will be solely determined by the rotation of earth). When doing long term calculations with closer bodies, however, other considerations must be taken into account. For example, the position of the Sun on the celestial sphere (i.e. in relation to all the other stars) is constantly shifting, moving a little under one degree eastward in each 24 hour period. The sun also moves due to the tilting of the earth on it's axis. The path traced by the sun on the celestial sphere is called the ecliptic.
The assumption of a celestial sphere makes it relatively easy to describe the position of a celestial body from the perspective of a person standing on the earth. The position of the sun, for example, can be related by two angles: the altitude is the angle between the sun and the observable horizon, whereas the the azimuth is the angle on the horizon measured clockwise from due south. From an observer on the earth's prospective, all points with the same altitude form a circle in the sky at that altitude, whereas all points with the same azimuth form a semicircle in the sky, passing directly overhead and intersecting the horizon at a right angles.

The method of representing points on a sphere that we have used here can be extended to spherical coordinates. You are no doubt accustomed to discussing points in 2-dimensional space, or the Euclidean plane as pairs of points (x,y). This idea can be extended by adding a third z-axis. Imagine that the xy-plane that you are used to lies on a chalkboard, the z axis will be coming directly out of the chalkboard, perpendicular to both the x and y axes. Now we can describe all points in three dimensional space as (x,y,z).
Spherical coordinates provide a different, and often useful way of describing the position of objects in three dimensional space. The basic principle of this coordinate system is that every point lies on some sphere centered at the origin, so one need only specify which sphere (using radius), and the precise coordinates of the point on said sphere (the angles of azimuth and altitude). Therefore a point is written in spherical coordinates as (r, θ, φ) where θ represents the azimuth, φ represents altitude, and r represents the distance between the point and the origin.