When a childhood friend of the Eppes brothers is found dead in the ocean, all initial signs point to a surfing accident. However, upon closer investigation, it becomes evident that a murder has occurred. A combination of FBI conducted interviews and Charlie's ingenuity result in the appropriate arrests.
Math plays a big role in this episode. Surfing relies on ocean waves and Charlie's understanding of waves allows him to determine the surfing conditions in different locations at different times. This knowledge allows the FBI team to deduce where the victim was killed and where to catch one of the perpetrators.
Charlie's solid understanding of waves allows him to, yet again, play a crucial role in the FBI's criminal investigation. In this section, we'll begin by discussing some general properties of waves and then focus our attention on wind waves in particular. You are encouraged to try out some (or all!) of the activities.
A wave in physics is loosely defined as a disturbance which propagates through space. It is usually the result of some transfer of energy. Light waves, sound waves and ocean waves all satisfy this description. However, because there are so many different types of waves, and it is difficult to discuss all of them at once, we will focus our attention on periodic waves. This way we can be more precise about definitions and characteristics.
A periodic wave is characterized by having (repeated) crests and troughs. It is either transverse or longitudinal. Transverse waves have their vibrations perpendicular to their direction of propagation. Longitudinal waves have their vibrations in the same direction as their direction of propagation. Light waves are transverse and sound waves are longitudinal.
Mathematically, a function f from the real line to itself is called periodic with period T if f(x+T) = f(x) for any real number x. Examples of such functions include g(x) = sin(x) and h(x) = cos(x). Notice that the graphs of these functions have crests and troughs and thus are periodic waves. However, not all periodic functions have graphs with crests and troughs. Can you think of any such periodic functions? Moreover, not all functions which have graphs with repeated crests and troughs are periodic functions; for example the graph of sin(x2) has crests and troughs but the function f(x) = sin(x2) is not a periodic function.
Let's take a closer look at the sine wave. This is used to model the motion of a simple harmonic oscillator. The function f(x) = sin(x) is periodic with period 2π and amplitude 1. (Recall that amplitude is half of the vertical distance between a neighboring crest and trough). It also has the property that f(0)=0 and f(-x) = -f(x) (i.e. it is an odd function). Alterations can be made to f(x) = sin(x) in order to change some of its properties. The next activity indicates a few of the things that can be done.
The following is an activity for those familiar with limits.
Finally, recall that the frequency of a periodic wave is defined to be the inverse of its period. That is, f = 1/T where f is frequency, and T is period. The unit of measurement for frequency is the Hertz (Hz). Note that 1 Hz = 1 period/second.
Now let's discuss a few basic properties of periodic waves in physics.
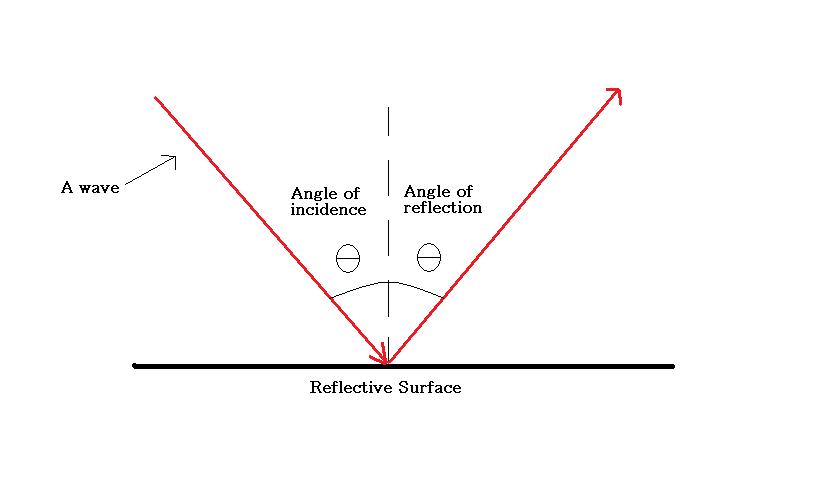
When a wave hits a reflective surface at an angle θ to the normal, it bounces off at an equal angle to the normal. That is, the angle of incidence is equal to the angle of reflection.
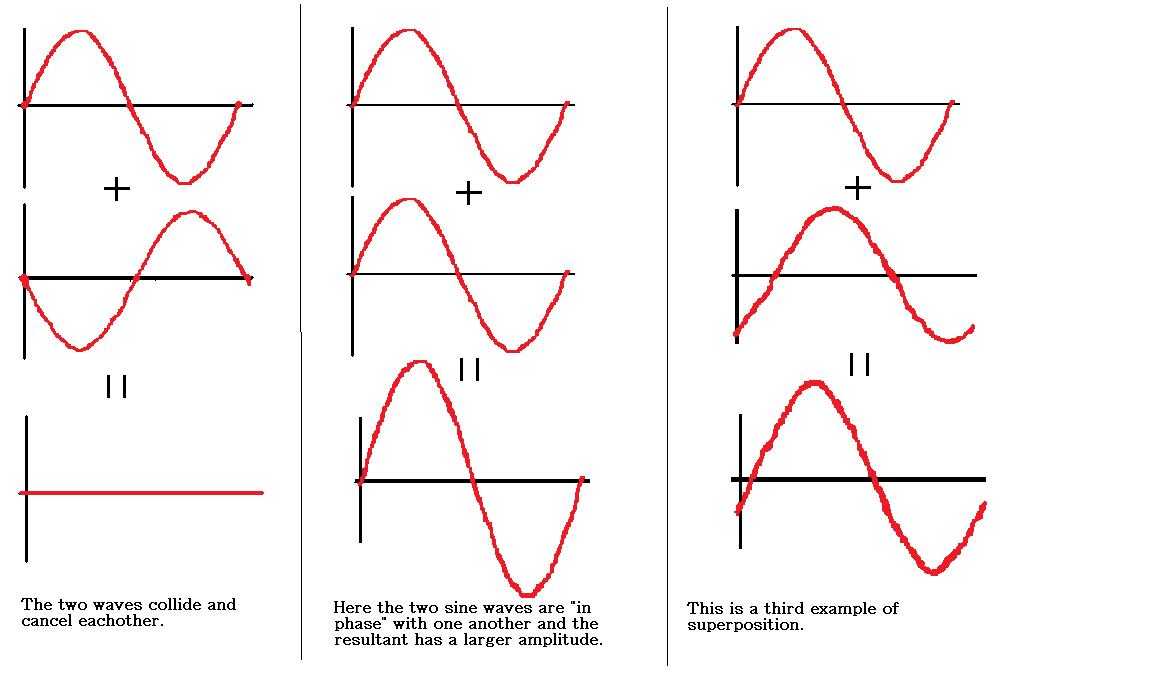
Superposition occurs when two waves collide with one another. The resultant wave is the sum of the two that come into contact. The following are a few examples of this phenomenon.
Refraction is the change in direction of a wave when its speed changes. This often occurs when a wave travels from one medium to another. Refraction occurs when you use eyeglasses, when a rainbow forms or when a straw appear to break into two pieces in a glass of water. Can you think of some other examples?
One can understand refraction across the boundary between two different mediums in a precise manner using Snell's Law (also known as the Law of Refraction). It states:
Here θ1 and θ2 denote the angle of incidence and refraction respectively. They are measured relative to the normal to the interface between the two mediums. v1 and v2 are the wave velocities in the first and second medium respectively. n1 and n2 are the refractive indices. Note that the refractive index for a given wave in a given medium is a measure of how much the wave slows down in that medium relative to a reference medium (ex: a vacuum for a light wave). For a light wave with wavelength 589nm, the refractive index for a vacuum is exactly 1. For air (at STP), it's 1.0002926 and for water (at 20oC), it's 1.3330. Knowing that refraction is the change in direction of a wave when its speed changes, the existence of a rule like Snell's Law should not come as a surprise. Notice that Snell's Law supports the fact that the refractive index for a wave in a medium is inversely proportional to its speed in that medium.
Here is another example of refraction:

This picture, created by NASA, shows white light being broken up into its spectrum of colors as it passes through a prism. The refractive index of the prism is different for different colors (or wavelengths) of light. Therefore, the different colors leave the prism at different angles. This creates a rainbow as seen in the picture. Note that the splitting up of a wave into its different frequencies (i.e. the different colors in this case) is known as dispersion.
Many waves that are seen on the surface of an ocean (or other body of water) are the generated by winds. Thus, these waves are called wind waves. In particular, the breaking waves that are used for surfing are wind waves. (Note that not all ocean waves are wind waves; for example, tsunamis are caused by geological factors and tides are caused by the gravitational pull of the moon and the sun.)

Many very different looking waves fall under the category of wind waves. They can be anything from tiny ripples to the huge breaking waves that crash into shore. There are three main types of wind waves. These are capillary waves, seas and swells. Capillary waves are the small ripples seen on the surface. They are caused by local winds and disappear soon after the wind stops blowing. Seas are wind waves that are again generated by local winds. Once the local winds die down, the waves that continue to propagate are known as swells.
When the base of a wave can no longer support its top, the wave collapses. These breaking waves are the waves that surfers ride. When a wave becomes too steep, it breaks. In deep water, waves break when wave height (the vertical distance between a neighboring crest and trough) divided by the wavelength exceeds 0.17. In shallow water, waves break when wave height divided by water depth is larger than 0.8.
Here are a few of the many places to learn more:
1. http://www.physicsclassroom.com/class/waves/U10l2a.cfmPlease note that the picture of the ocean wave above is from website 4. Further authorship information can be found there.