Here F is force, m is mass and a is acceleration.
In this episode, a train crash occurs causing fatalities and a leak of toxic chemicals. It's up to the FBI team to help rescue the living victims as well as figure out the cause of the crash. Math and physics play a role in both of these tasks.
In order to help rescue the living victims in one of the rail cars, Charlie uses small robotic cars known as swarm bots to survey the situation and map out a route for the rescue team. To determine the cause of the crash, Charlie utilizes some basic physics to deduce that the conductor was lied to about the mass of the train and cargo.
In this website, we'll focus on some of the math and physics that Charlie needs in order to figure out the cause of the crash. However, if you wish to learn about swarm robotics, the following are a few places to begin.
1. http://www.swarm-robotics.org/Suppose an object is moving along a straight line. We can fix a reference point and graph the position of the object (relative to this reference point) over time. Let s(t) denote the function which has this graph. The value of s at a given time t* is the displacement of the object at time t*. For example, if s(t*)=5 then the object is 5 units in front of the reference point at time t*. If s(t*)= -5, then, at time t*, the object is 5 units behind the reference point. Therefore, if t1 and t2 (with t1 < t2) are two times, we have that the average velocity of the object between time t1 and t2 is
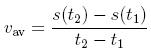
If Δt=t2-t1, we can rewrite the above equation as
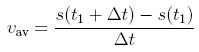
For those of you that are familiar with basic calculus, notice that the formula for average velocity would look like the definition of a derivative if there were a limit thrown in. In fact, if we take the limit as Δt goes to 0, we obtain instantaneous velocity at time t1. That is,

Analogously, we can define average acceleration (over time Δt) and instantaneous acceleration (at time t) by
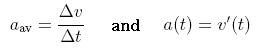
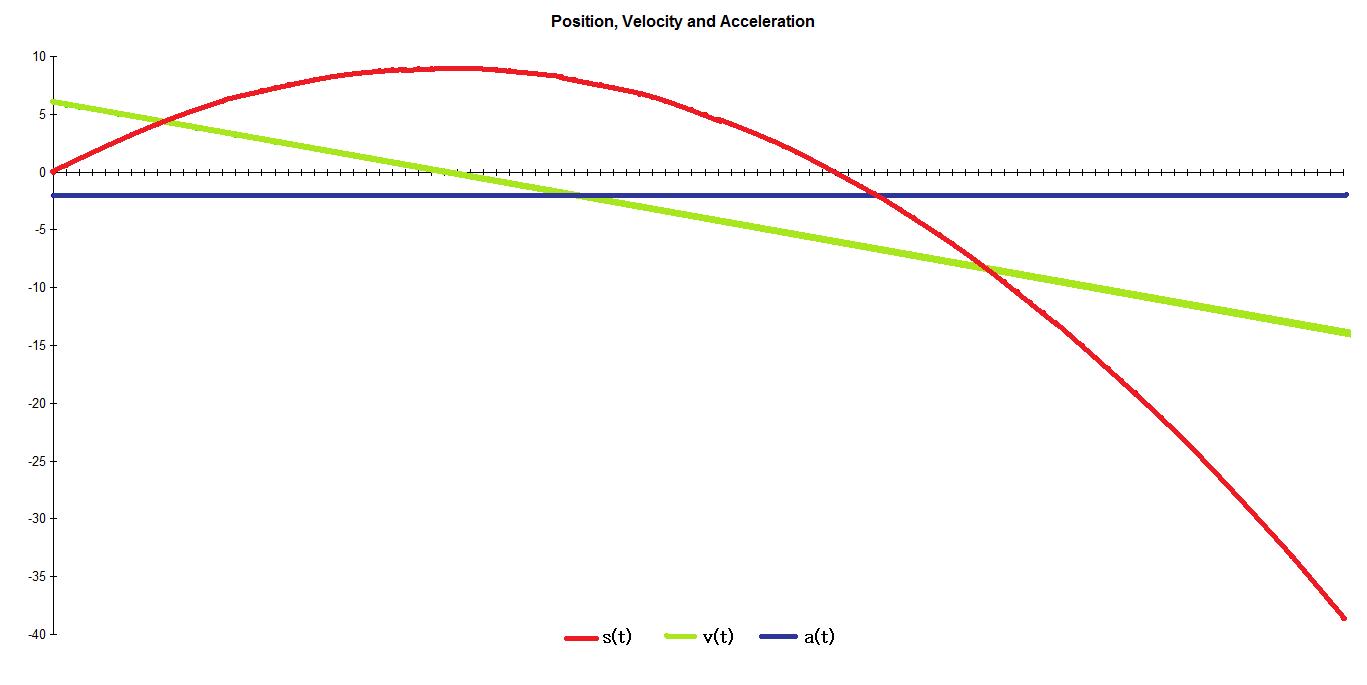
Let's consider the example s(t) = -(t-3)2 + 9. This describes the motion of an object which is at the reference point at t=0, then moves forward, changes direction and eventually ends up behind the reference point. We also have that v(t)=-2(t-3) and that a(t) = -2. That is, the object with position described by the function s(t) has constant acceleration. Below are the graphs of s(t), v(t) and a(t).
When acceleration is constant, one can derive equations of (linear) motion by solving the differential equations described above. For example, consider the equation a(t)=v'(t). If acceleration is a constant a then we have the equation a = v'(t). Separating variables and integrating from ti to t yields the equation a⋅(t-ti) = v(t) - v(ti). Thus, if we put Δt = t-ti and vi=v(ti), we have that v(t) = vi+aΔt. Using similar techniques, we can get the following equations of linear motion:
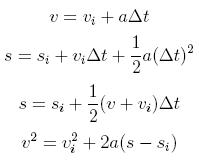
One final remark is needed: Be sure to be consistant with units when using the equations of motion! For example, don't measure acceleration in m/s2 and velocity in km/h. Either measure both quantities using meters and seconds or both using kilometers and hours.
Force is a vector quantity. That is, like velocity and acceleration above, it has both a magnitude and direction. When a force is applied to an object, it causes the object
to accelerate in the direction of the applied force. The relationship between force and acceleration can be made precise with the famous equation
![]()
Here F is force, m is mass and a is acceleration.
Of course, many forces can act on the same object. It is even possible that the net force (i.e. the vector sum of all of the forces acting on the object) is 0. In this case, the object will stay put. When multiple forces act on an object we have the equation
A free body diagram is helpful in keeping track of all the forces that act on an object. It is a diagram where the object is represented by a box (or other simple shape) and includes arrows of different lengths and directions to represent the various forces that act on the object. Below is an example of a free body diagram for an object being pushed along a table by an applied force F_a. F_g, F_N and F_f denote force of gravity, normal force and force of friction respectively.
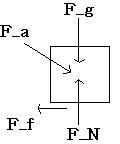
The SI unit for force is the newton (N). One newton is equal to one kg⋅m/s2. It is again very important to be careful with units when using the force equations above.
Here are some references and places to learn more:
1. Giancoli, Douglas C. Physics for Scientists & Engineers, Third Edition. Prentice Hall, 2000.