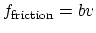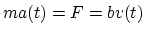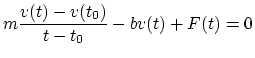Numb3rs 217: Mind Games
The two mathematically significant moments in this episode are the
card-color guessing game to which Agent Reeves challenges the psychic
and Charlie's use of the Fokker-Planck equation in an attempt to
determine where migrants are likely to be found. Both are based on
the science of probability.
Psychic Testing 101
Suppose one day, out of the blue, a friend calls you up and claims to
have acquired psychic abilities, like the ability to see things
telepathically, without physically observing them. You are naturally
curious, and so you decide to test your friend by making him guess the
color of cards he can't see, much like Agent Reeves tested the alleged
remote-seer in the
episode.
To avoid bias and reduce the possibility of
cheating, scientists usually conduct
double
blind trials, where neither the subject nor
the experimenter know
at the time of experiment which answers are correct and which
are not. In your case, you might put the cards in identical
envelopes, shuffle them, and only open each envelope following
your friend's guess.
The idea of this experiment is that while a good guesser might pick the
color correctly once, twice, or even three or four times in a row,
after enough correct answers you'll become convinced that something other
than guessing is going on. How convinced and at what point? Let's find
out.
Activity 1: First we should agree on notation.
I'll denote by p(
n;
m) the probability of a person
guessing at random the color of
m cards correctly out of
a total of
n cards. What are the values of the following?
- p(1;1)
- p(1;0)
- p(2;2) (Hint: recall that the probability of two independent
events occurring is
the product of their probabilities)
- p(2;1)
- p(n;n), where n is any positive
integer.
- Is p(n;n)=p(n;0) for every positive
integer n?
One way to answer #4 above is to look at the order of choices.
Guessing one color correctly and another wrongly can be done by guessing
the color of the first card and not of the second (0.5*0.5=0.25) or by
missing the color of the first card and correctly identifying the color
of the second card (another 0.5*0.5=0.25) for a total probability of
0.5. This case analysis can be generalized if we make one crucial
observation. Suppose the cards are put into envelopes which are
numbered 1 through n, and suppose further that someone randomly
guesses the color of each card. You then open the envelopes and record
a sequence of n results, ordered by the numbers on the envelopes.
For n=4 for instance, you might get the sequence
(RIGHT WRONG WRONG RIGHT)
corresponding to correct guesses for the cards in envelopes 1 and 4, and
incorrect guesses for 2 and 3. Since the guesses are independent
events, and each has a probability of 0.5 of being correct, each
particular ordered sequence of rights and wrongs has an equal
probability of occurring as any other, that is
0.5n, for n guesses made. Thus to
find p(n;m) all we must do is calculate the number of
different ordered sequences of length n with m right
guesses and n-m wrong, from now on denoted C(n,m),
and multiply it by the probability of each occurring, i.e.
0.5n. Putting all this into one equation,
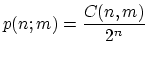
Activity 2: What is C(n,m)?
- Suppose you have before you n white marbles, numbered
consecutively from 1 to n. How many different ordered sequences
of numbers can you produce by arranging the marbles side by side
into an ordered sequence? (Hint: imagine that you start out
with n marked spots on which you place the marbles to
make your sequence. Then you have n different spots to
place the first marble on, n-1 spots to place the second
marble, n-2 for the third, and so on.)
- Now we change the procedure a bit: we color the first
m numbered marbles red, and the remaining n-m
blue. We also separate the red and blue numbered marbles. How
many different pairs of ordered sequences are there
corresponding to separate arrangements of red and blue
marbles? (Hint: for every ordered arrangement of red marbles,
how many different ordered arrangements of blue marbles are
there?)
The connection between the above two questions and the value of
C(n,m) is the following: to make an ordered sequence of
numbered marbled as in #1 above we can first color the marbles one of
two colors, as in #2, then arrange the marbles of each colors into two
separate colored sequences, and finally put those two sequences together
according to a length n sequence of R's and
B's corresponding to the number of red and blue marbles (see
illustration below).
.png)
Thus we get that the number of arrangements in #1, n!, is equal
to the number of arrangements in #2 times the number of different
sequences of length n of m R's and n-m B's, that is
C(n,m). And so we arrive at the sought out answer,
n!=m!(n-m)!C(n,m), implying
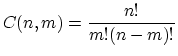
Activity 3:
- What are the values of p(20;8) and p(20;12)? How about
p(13;6) and p(13;7)?
- Can you see a pattern? Why does it occur?
Activity 4:
- What's the probability of guessing
at random the color of 15 or more out of 20 cards?
- What about 10 or more, out of 20?
- How about 9 or less?
- What's the connection between the last two answers?
Now you're ready to test your friend's claims, having at your disposal
the ability to tell how likely a particular result is if the guesses are
random. How many colors of cards would your friend need to correctly
identify, say out of a total of 20, in order to convince you that
he's not just randomly guessing?
Despite wide public fascination with psychic phenomena, no one
has yet been able to achieve a statistically significant result
in tests like the one above (i.e. consistently doing better than
random guessing). For the last few decades the magician James
Randi has been
offering a
million dollars for any demonstration of paranormal
powers. Nobody has won this prize so far.
Meet the Fokker-Planck
 Actually, the story begins with neither Fokker nor Planck, but Einstein,
who in 1905 published a paper about a very curious phenomenon observed
by botanist Robert
Brown almost a century earlier. As he was looking at pollen submerged
in water under a microscope, Brown noticed tiny particles--much smaller
than the pollen grains themselves--moving in seemingly random manner in
the water. He confirmed that this motion did not depend on the type of
particles submerged, just on their minuscule size. The science of the
time could not explain this; the missing ingredient was the atomic and
molecular model of matter, developed only toward the end of the 19th
century
Actually, the story begins with neither Fokker nor Planck, but Einstein,
who in 1905 published a paper about a very curious phenomenon observed
by botanist Robert
Brown almost a century earlier. As he was looking at pollen submerged
in water under a microscope, Brown noticed tiny particles--much smaller
than the pollen grains themselves--moving in seemingly random manner in
the water. He confirmed that this motion did not depend on the type of
particles submerged, just on their minuscule size. The science of the
time could not explain this; the missing ingredient was the atomic and
molecular model of matter, developed only toward the end of the 19th
century
Armed with the newly developed molecular theory of matter, Einstein
proposed the following simple solution: the fact that the water has
positive temperature just means that water molecules are moving around,
and if the submerged particle is small enough, it gets pushed around by
the molecules.
.png) Consider a top-down view of a small particle of mass m immersed
in water, moving with some velocity v(t) at time t, as in
the picture below. We ignore the force of gravity pulling it down and
buoyancy
pushing it up; we're only interested in motion in the horizontal plane.
In this case, the only force acting on the particle is drag, the
friction force of water. This force is proportional to the velocity v,
that is,
Consider a top-down view of a small particle of mass m immersed
in water, moving with some velocity v(t) at time t, as in
the picture below. We ignore the force of gravity pulling it down and
buoyancy
pushing it up; we're only interested in motion in the horizontal plane.
In this case, the only force acting on the particle is drag, the
friction force of water. This force is proportional to the velocity v,
that is,
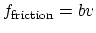
for some positive constant b depending on the
shape of the particle.
Thus, by Newton's
second law of motion, we have
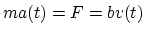
where
a(t) is the acceleration at time t. Since acceleration is
just the change in velocity, we get the equation

Activity 1: Suppose our particle starts out at time t=0
moving North with velocity v(0), with no external force acting
on it. Why do the following velocity
equations v(t) fail to fit our model?
- v(t)=cos(t)/t
- v(t)=3t2+t+1
- v(t)=5-t for 0≤t≤5, and v(t)=0 for t≥5.
Solving the equation

for v(t) as
t-t0 becomes small, we get

Activity 2*: If you know calculus, first
show that this solution fits the equation, then derive it
yourself.
Activity 3: Suppose m=8, b=3 and the
velocity at time zero is v(0)=5m/s. When will the velocity
decrease to less than
1m/s? Less than 0.1m/s?
Thus as we expect, the speed of the particle decreases to zero. If the
particle is relatively massive then this is the end of the story: given
the initial velocity, you can calculate where the particle will be at
time t and its velocity at that time. However, if the particle
is small enough, it will get pushed around by water molecules bumping
into it, and the above description is no longer accurate.
Given a small enough particle, each collision with a water molecule will
result in a transfer of momentum. That
is, the colliding molecule will exert a force on our particle for the
very short duration of collision, leading to a change in the particle's
velocity. Since thousands such collisions occur each second, it's
practically impossible to account for the movement of every molecule and
solve the resulting system of equations to find out what exact effect
the collisions will have on our particle. Thus we do the next best
thing: approximate this effect by a "random" fluctuating force F(t), so
our equation becomes
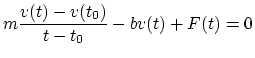
The Fokker-Plank equation is based on a generalization of this
assumption, where given data about what the random component of the
motion is like (called diffusion term), and knowing the few
non-random forces acting on the particle (the drift
terms), the equation allows you to figure out what is
the probability of a particle being in a certain area at a future time.
This idea can be applied to any situation in which a quantity, for
instance the population of parrots on an island, is subject to known
deterministic forces--availability of food, presence of predators--and
smaller, but significant "randomly fluctuating" forces--like weather
pattern changes for instance.
.png)
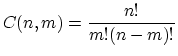
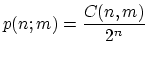
 Actually, the story begins with neither Fokker nor Planck, but Einstein,
who in 1905 published a paper about a very curious phenomenon observed
by botanist Robert
Brown almost a century earlier. As he was looking at pollen submerged
in water under a microscope, Brown noticed tiny particles--much smaller
than the pollen grains themselves--moving in seemingly random manner in
the water. He confirmed that this motion did not depend on the type of
particles submerged, just on their minuscule size. The science of the
time could not explain this; the missing ingredient was the atomic and
molecular model of matter, developed only toward the end of the 19th
century
Actually, the story begins with neither Fokker nor Planck, but Einstein,
who in 1905 published a paper about a very curious phenomenon observed
by botanist Robert
Brown almost a century earlier. As he was looking at pollen submerged
in water under a microscope, Brown noticed tiny particles--much smaller
than the pollen grains themselves--moving in seemingly random manner in
the water. He confirmed that this motion did not depend on the type of
particles submerged, just on their minuscule size. The science of the
time could not explain this; the missing ingredient was the atomic and
molecular model of matter, developed only toward the end of the 19th
century.png) Consider a top-down view of a small particle of mass m immersed
in water, moving with some velocity v(t) at time t, as in
the picture below. We ignore the force of gravity pulling it down and
Consider a top-down view of a small particle of mass m immersed
in water, moving with some velocity v(t) at time t, as in
the picture below. We ignore the force of gravity pulling it down and