Numb3rs 219: Dark Matter
In this episode Charlie uses a support vector classifier in an
attempt to identify the remaining school shooter. A support vector
classifier, or rather support vector machine (SVM), as it's more
commonly known, is a method for classifying objects described by a given
set of properties into groups. While this definition may leave
you underwhelmed, keep in mind that the problem of classification lies
at the heart of intelligent behavior. It takes you a split of looking
at a photo to recognize a tree, a car, a friend, but for a computer,
image classification is a very hard task indeed. On the flip side of
the coin, it may take an FBI agent weeks or months to pour over records
and decide which individuals most closely fit the profile of a
school shooter, but a well designed SVM may do so in seconds or
minutes. Making SVMs do things like image or voice recognition quickly
and accurately is a currently hot research topics in artificial
intelligence. So how do SVMs work? Let's find out!
Vectors, Matrices, and the Stuff They Do
Before we can explore SVMs, we need some understanding of vectors and
matrices. (Actually, if you only want to understand the introduction to
SVMs contained in the following section, you only need to know what
vectors are and what a dot procuct
is. If you wish to learn more about SVMs, or are interested in learning
a fundamental tool of mathematics, you ought to master the material on
matrices below.)
.png) A vector is simply an ordered list of numbers, called
coordinates. For instance,
(2, 5) is a 2-vector, i.e. a vector of dimension 2, while (-3, 1.4, 5)
is a 3-vector. Usually vectors are represented as arrows in the Euclidean
space of the corresponding dimension: arrows starting at the
origin and ending at the point corresponding to the coordinates, as in
the picture to the right. At other times vectors are represented simply
by the point corresponding to their coordinates, to avoid cluttering the
picture.
Vectors of the same dimension can be added and subtracted, simply by
adding and subtracting the pairs of corresponding coordinates:
(2, 5)+(-4, 3.3)=(-2, 8.3).
Vectors can also be multiplied by a number, by multiplying each
coordinate by that number: -4*(2, 5)=(-8, -20).
A vector is simply an ordered list of numbers, called
coordinates. For instance,
(2, 5) is a 2-vector, i.e. a vector of dimension 2, while (-3, 1.4, 5)
is a 3-vector. Usually vectors are represented as arrows in the Euclidean
space of the corresponding dimension: arrows starting at the
origin and ending at the point corresponding to the coordinates, as in
the picture to the right. At other times vectors are represented simply
by the point corresponding to their coordinates, to avoid cluttering the
picture.
Vectors of the same dimension can be added and subtracted, simply by
adding and subtracting the pairs of corresponding coordinates:
(2, 5)+(-4, 3.3)=(-2, 8.3).
Vectors can also be multiplied by a number, by multiplying each
coordinate by that number: -4*(2, 5)=(-8, -20).
.png) Activity 1
Activity 1: To the right
you see the geometric representation of vector addition. What
geometric figure do the blue vector lines and dotted lines
produce? Draw a similar diagram for vector subtraction, say for
(5, 1)-(1, 2)=(4, -1) and find the corresponding parallelogram.
A matrix is an array of vectors stacked on top of each
other. One way to think of it is as a vector of vectors. The first
matrix below is a 2x3 matrix (2 rows, 3 columns), while the second is
4x2.
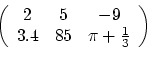
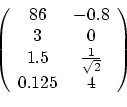
When multiplying a matrix by a number, you simply multiply each
entry by that number, just like for vectors. Two matrices of the same
size can be added together by adding the corresponding entries, just
like for vectors.
Multiplying a matrix by a vector is the same as multiplying a matrix
by another matrix, with one of them having only one row or column. Now
we have to differentiate between column vectors, which are
matrices with one column, and row vectors, which are matrices
with one row. Thus a 3x2 matrix A can be multiplied by a row
3-vector (a 1x3 matrix) as VA, resulting in a row 2-vector, or by a
column 2-vector (a 2x1 matrix) on the right, as AV, resulting
in a column 3-vector (see example below).
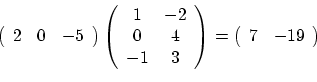
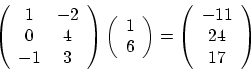
Usually vector means column vector, but not always, so pay attention to
the context.
Activity 3:
- What happens when you multiply a (column) 2-vector (2x1
matrix) by
 ? How about a row 2-vector?
Draw it.
? How about a row 2-vector?
Draw it.
- What happens when you multiply a 2-vector by
 ? Draw it.
? Draw it.
- The dot product of two vectors v and w of the same
dimension, denoted v·w, is simply their product as
matrices when you consider v to be a row vector and w a column
vector. Thus the dot product of two vectors is always a number
(a 1x1 matrix). What is the dot product of v=(3,-1,6) and
w=(-1, -3, 7)? What about w·v?
- For n a positive integer, is it always the case that for any
two n-vectors v and w, v·w=w·v?
Activity 4:
- The length of a vector v is defined as the square
root of v·v, and is usually denoted ||v||. Why is this a
good definition? (hint: think
Pythagoras)
- The distance between two vectors v and w (of the same
dimension) is defined as ||v-w||. Is ||v-w||=||w-v|| for all
vectors v and w?
Now that you've done the activities above, we have a new way of
thinking of matrices. You can think of a function of one variable, say
f(x)=2x+5, as a machine into which you feed a number, x, and get back a
different number 2x+5. For a two variable function, f(x,y)=x+y say, you
feed in two numbers, x and y, to get back one, x+y. With matrices
things get more interesting: you feed in a vector and get back a
vector!
Activity 5*: If you
know a bit about vector
spaces, or are interested in learning about them, try answering
the following question. Why is matrix multiplication
defined the way it is? (Hint: if you find this question
challenging, and you likely will, ask a math teacher for help,
or consult any book on linear algebra. Look up vector spaces
and linear transformations.)
Support Vector Machines
Suppose you want to teach a computer to differentiate between a
handwritten digit 1 and a handwritten 0. First you gather
a sample of say 50 handwritten ones and 50 handwritten zeroes,
from different people, and scan them to produce digital images, each
measuring 100 by 100 pixels. Every pixel has a color, which is
given by a non-negative integer. Thus you can represent each scanned
digit image as a 10000-vector: each pixel corresponding to one
vector coordinate and that pixel's color corresponding to the numeric
value of the coordinate. For instance, if we have only 256 colors, a
"picture" consisting of 4 pixels can be represented by a 4-vector, each
coordinate of which can take on values from 0 to 255. The problem is
then to find a rule using which a computer, given a new 10000-vector,
can decide whether the vector represents a picture of a 0 or a 1.
Activity 1: Let's make life easier for
ourselves and examine the case of 2-vectors, which we will draw
as points on the Cartesian plane (we'll have a whole bunch of
them, so drawing arrows is impractical).
- Suppose you ask 40 random participants in this year's Boston
Marathon their height and time spent training
per week. You then divide them into two groups, those that
completed the marathon and those that did not and plot this
data as in Figure 1 below. Based on this data, if I give
you the height and weekly training time of another runner,
could you tell whether the runner is likely to complete next
year's marathon? How confident would you be in this prediction?
What if I only tell you the runner's height? How about if you
only know the weekly training time?
- How about the data vectors in Figure 2? Given a new vector
(a new data point) how confident will you be in
guessing to which group it belongs? What if you simply know
that the x component of a new vector, without knowing the y
component?
- How does the data in figures 3 and 4 differ? In what case
is classification easier?
.png)
As you've seen in the activities above, in some cases the
classification problem is easier, in others harder or impossible. The
basic idea behind SVMs is to use lines for 2-vector data and planes for
3-vector data (in general hyperplanes)
to divide the space in which the vectors live into two "halves": a half
in which only vectors from one group are located and a half in which
vectors from the other group lie. New vectors are then classified
depending on which half they lie in. For
2-vectors and lines, this is sometimes possible, as in the case of
Figure 2 above, and sometimes not, as in the case of Figure 1. That is,
you can't
separate the two vector groups in Figure 1 by a line while you can in
Figure 2. In the case where you can separate data groups by a line, how
do you find the best line that separates the data? Good question!
Let's proceed to activity 2.
.png)
.png) Activity 2
Activity 2:
- Two vectors v and w are called orthogonal when
their dot product v·w is zero. Find a vector orthogonal
to (5,3). Find a different one. Draw all three vectors.
- One way to define a line through the origin on the Cartesian
plane is by specifying a normal vector v, i.e. a vector
to which all points on the line are orthogonal (see right).
What vector is normal to the x-axis? To the x=y line?
- We can use the above idea to define a line through the
original by an equation such as (x,y)·(-3,-2)=0. Convert
this equation to the usual
slope-intercept
form for an equation of a line. Write a different dot product
equation for this line (i.e. use a vector different from
(-3,-2), and again convert it to slope-intercept form.
- Now we know how to write lines through the origin in terms
of normal vectors. What about lines not passing through the
origin? The key observation is that such lines are simply lines
through the origins shifted over in some direction. Draw the
line corresponding to (x,y)·(3,4)+5=0. What's the dot
product equation of the line y=7x+2?
- Where is the region (x,y)·(-1,2)+4<0 located? How
about (x,y)·(0,1)+10>0?
.png)
The distance from a vector v to a line given by (x,y)·w+c=0,
where w is a 2-vector and c a number, is defined as the shortest
distance between v and any point on the line and is equal to 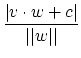 . Note
that in the numerator |v·w+c| means absolute value, while in the
denominator ||w|| means the length of the vector w. Suppose
our initial data is given by vectors v1,
v2, ... ,vk, each belonging to groups 1 or 2.
Using the ideas above, we can think of finding the best separating line
by finding a 2-vector w and a number c such that
. Note
that in the numerator |v·w+c| means absolute value, while in the
denominator ||w|| means the length of the vector w. Suppose
our initial data is given by vectors v1,
v2, ... ,vk, each belonging to groups 1 or 2.
Using the ideas above, we can think of finding the best separating line
by finding a 2-vector w and a number c such that
- the line (x,y)·w+c=0 separates the two groups of
vectors
- the distance from the line to the closest vector in group
1, call it d1, plus the distance to the closest
vector of group 2, call it d2, is the largest
possible
One this is done, we can equalize d1 and d2 by
changing c, i.e. moving the line up or down.
Vectors of distance d1=d2 from the separating line
are called support vectors.
Visually, the picture looks something like the one on the right. Note
that if you add/remove data points that are further from the separating
line than the support vectors, the separating line will not change;
thus, in some sense, only the support vectors matter.
So how are such vector w and number c actually found? Mostly by
various numerical methods: by turning this problem into a form which
computers can use to find a good approximation to the solution.
.png)
All right, so now we know the idea behind SVMs: find a separating line
(or hyperplane, in the general n-vector data case) and classify new
vectors based on which side of the line they fall on. What about a
situation similar to Figure 1 in Activity 1, where it's impossible to
separate the data with a line? There are a few approaches. The most
simple one is to separate the data to the best possible degree. That
is, allow vectors in both groups to be located on both sides of the
"separating" line, but minimize the resulting error: find a line so as
to minimize the distances to the vectors located on the wrong side (see
illustration to the right).
This method, however, would give terrible results in cases like that of
Figure 3, where the data is "separable" but not by a line! This is
where the real magic happens: what we do is map our data to a higher
dimensional space in such a way that in the new space we can separate
it with a plane. For the data in Figure 3 for instance, one way to do
this is to use a map like f(x,y)=x2+y2. See the
illustration below.
.png)
Activity 3*:
.png)
- Find a map f such that the data to the right will be
separable by a line when mapped to the points (x,f(x)) in the
plane (hint: think trigonometry).
- What do the two separated regions look like when mapped
back to the real line?
When the initial data vectors are easy to visualize, such as in the case
of the above examples of vectors in the plane, it's often easy to find a
map to a higher dimensional space where the data can be separated.
However, in real world applications, such as handwriting recognition
which I described earlier, it's not feasible to "look" at 1000-vectors
and "see" the suitable map. Thus much of the current research in SVMs
focuses on finding good generic maps, often to very high
dimensional spaces (or even infinitely dimensional), which produce good
results for whole categories of initial data, like the category of
written characters or the category of speech recognition.
.png) A vector is simply an ordered list of numbers, called
coordinates. For instance,
(2, 5) is a 2-vector, i.e. a vector of dimension 2, while (-3, 1.4, 5)
is a 3-vector. Usually vectors are represented as arrows in the Euclidean
space of the corresponding dimension: arrows starting at the
origin and ending at the point corresponding to the coordinates, as in
the picture to the right. At other times vectors are represented simply
by the point corresponding to their coordinates, to avoid cluttering the
picture.
Vectors of the same dimension can be added and subtracted, simply by
adding and subtracting the pairs of corresponding coordinates:
(2, 5)+(-4, 3.3)=(-2, 8.3).
Vectors can also be multiplied by a number, by multiplying each
coordinate by that number: -4*(2, 5)=(-8, -20).
A vector is simply an ordered list of numbers, called
coordinates. For instance,
(2, 5) is a 2-vector, i.e. a vector of dimension 2, while (-3, 1.4, 5)
is a 3-vector. Usually vectors are represented as arrows in the Euclidean
space of the corresponding dimension: arrows starting at the
origin and ending at the point corresponding to the coordinates, as in
the picture to the right. At other times vectors are represented simply
by the point corresponding to their coordinates, to avoid cluttering the
picture.
Vectors of the same dimension can be added and subtracted, simply by
adding and subtracting the pairs of corresponding coordinates:
(2, 5)+(-4, 3.3)=(-2, 8.3).
Vectors can also be multiplied by a number, by multiplying each
coordinate by that number: -4*(2, 5)=(-8, -20)..png) Activity 1: To the right
you see the geometric representation of vector addition. What
geometric figure do the blue vector lines and dotted lines
produce? Draw a similar diagram for vector subtraction, say for
(5, 1)-(1, 2)=(4, -1) and find the corresponding parallelogram.
Activity 1: To the right
you see the geometric representation of vector addition. What
geometric figure do the blue vector lines and dotted lines
produce? Draw a similar diagram for vector subtraction, say for
(5, 1)-(1, 2)=(4, -1) and find the corresponding parallelogram.
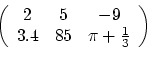
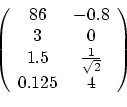
 . What's
the result? What if you start out with a different 2x2
matrix? Does AB=BA?
. What's
the result? What if you start out with a different 2x2
matrix? Does AB=BA? do? Does multiplying on the
right give the same result as multiplying on the left?
do? Does multiplying on the
right give the same result as multiplying on the left? . Do it again with a
different starting matrix. What's happening? What if you
change the order of multiplication?
. Do it again with a
different starting matrix. What's happening? What if you
change the order of multiplication?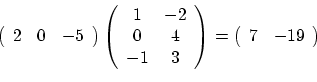
.png)
.png)
.png) Activity 2:
Activity 2:
.png)
 . Note
that in the numerator |v·w+c| means absolute value, while in the
denominator ||w|| means the length of the vector w. Suppose
our initial data is given by vectors v1,
v2, ... ,vk, each belonging to groups 1 or 2.
Using the ideas above, we can think of finding the best separating line
by finding a 2-vector w and a number c such that
. Note
that in the numerator |v·w+c| means absolute value, while in the
denominator ||w|| means the length of the vector w. Suppose
our initial data is given by vectors v1,
v2, ... ,vk, each belonging to groups 1 or 2.
Using the ideas above, we can think of finding the best separating line
by finding a 2-vector w and a number c such that .png)
.png)
.png)