Numb3rs 220: Guns and Roses
Alas, there's little actual mathematics in this episode, so we'll
explore the next best thing: some physics. In particular, we'll look at
the Doppler effect, what it is, when it occurs, and how we can use
it.
The Frequencies they are A-changin'
You've probably noticed the Doppler effect many times before. It's the
change of a siren's pitch you hear as an ambulance or a firetruck passes
by you. To understand why in such situations we hear the pitch change
we must first learn a little about waves.
A light wave (or
electromagnetic
wave, as it's
properly called) differs from other types of waves in that it
does not require a medium in which to propagate: electromagnetic
waves travel through empty space, while for example sounds waves
can only travel through a gas, liquid, or a solid. Another,
related peculiarity of electromagnetic waves is that they act
both like waves and like particles! This puzzling phenomenon
has motivated much of the development of modern physics and the
discovery that
all particles
have
wave-like properties.
A traveling wave, whether occurring in water (e.g. sea wave), air (sound
wave), or vacuum (light wave), looks something like this
in action (courtesy of wikipedia). You can see a snapshot
representation of a wave to the left below. The distance
between two consecutive peaks or troughs is called the
wavelength is usually represented by the Greek letter lambda
(λ). The time it takes for a wave to travel one wavelength, the
distance λ, is called a period, and we'll denote it by
T. In the picture to the right below, a source is
producing a continuous wave of a given wavelength. The
circles represent the peaks of the wave, the distance between them
equaling the wavelength.
.png)
Activity 1:
- What is the relation between a wave's speed, wavelength,
and period? (Hint: it's not hard, try. If you're stuck, look here.)
- The quantity 1/T is called the frequency of the
wave. It corresponds to the pitch we hear when a sound wave
hits our eardrums and the color we see when a light wave hits
the retina.
Rewrite the above relation in terms of frequency instead of
period.
Suppose now that the source of the wave is moving toward you, as in
the picture in activity 2 below. While the source is
still emitting a fixed frequency wave, the perceived wavelength now
depends on
where the observer is located with respect to the source.
.png) Activity 2
Activity 2:
- Assume the source is moving toward you, the observer, with
speed v0, and the wave emitted is a sound
wave of frequency f. Then the corresponding wavelength
λ, by activity 1 above, is equal to
vs/f, where vs is the speed of sound in
air (around 345 meters/second). What does the perceived
wavelength λ' equal to in terms of v0, T, and
λ?
- What does λ' equal to in terms of the speed of sound
vs and the perceived frequency, which we'll
denote f’? (Hint: use
activity 1.)
- Write the equation from part 1 above in terms of f,
f’, vs and v0.
If you did the algebra correctly, you should have gotten something
equivalent to
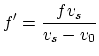
for #3 above. What this tells us is that perceived sound frequency, the
pitch, increases relative to the original frequency as v0
increases.
Activity 3:
- Suppose that instead of moving toward you, the source of the
sound moves away from you with speed v0. How does
the equation for the perceived frequency f’ change?
- What happens if the sound source is stationary, but you, the
observer, are moving toward it with speed v0? Draw
a picture, work it out!
- What if the sound source approaches you with a speed greater
than vs? I.e. what if v0 ≥
vs?
 Activity 4
Activity 4:
- Suppose you're standing by a sound source which emits a
a single frequency tone for a split second. How fast will you
need to run away from the sound source to hear the tone for as
long as you keep running? (Ignore the issue of volume, which
corresponds, by the way, to a
wave's amplitude
or height.)
- The orchestra has just finished playing Beethoven's
5th symphony, and you, a member of the audience,
suddenly feel a strong urge to hear it again, but backwards!
How fast would you have to run away from the concert hall to
hear it replayed from finish to start at the pitch it was
originally performed?
As you may have noticed, we have so far ducked the original question!
All of the above discussion does not explain why we hear the pitch of a
siren change as it passes us. The reason is that we, the observer, are
not in the path of the sound source as that happens: the ambulance
passes by us, not through us (one may hope). Thus while the pitch did
not change for the observers in the diagram in activity 2, it would if
the observers were not on the line of motion, as in the illustration to
the right. The key to describing how the perceived frequency changes is
to note that we only care about the speed of the source relative to the
observer. Thus the only modification needed is to figure out what this
speed is in the case where the observer is not on the line of
motion (see illustration below).
.png)
.png) Activity 5
Activity 5:
- Recall a bit of trigonometry: in a right triangle to the
right, what is length of side a in terms of angle θ and
the hypotenuse c?
- As in the picture above, the sound source is moving West
with speed v0. What is the speed of the source
relative to the observer at an angle θ North of it? (Hint:
use part one and see illustration above.)
.png) Activity 2:
Activity 2:
.png)
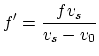
 Activity 4:
Activity 4:
.png)
.png) Activity 5:
Activity 5: