In this episode, Charlie lectures about the Riemann Hypothesis in his graduate number theory course.
A positive whole number is a prime if it has only 2 positive integer divisors: 1 and itself. For instance, 3 and 7 are primes because no other numbers besides 1 and 3 and 7, respectively, evenly divide the two. 1 is not a prime because it has only one positive integer divisor, itself. 1 is called a unit. 4 is also not a prime number because it is the product of 2 with itself. Positive integers that are not prime and not 1 are called composites because they can be composed with primes, as shown by the fundamental theorem of arithmetic.
The fundamental theorem of arithmetic states that every positive integer can be uniquely factored into some finite number of primes, with possible duplication. For instance, 
. 24 is the product of three 2's and one 3. Both 2 and 3 are primes, and 24 cannot be represented any other way as a product of these primes or different primes.
The fundamental theorem of arithmetic may seem trivial or obvious, but the same statement is not true for all numbering systems. Consider the numbers of the form 
where 
and 
are integers. This set of complex, when plotted on the complex plane looks like an infinite rectangular lattice of points - the vertices of rectangles if one was to tile the plane completely with them. The sum or difference of a number of this form is still a number of this form, and the product of two of these is again of this form. These operations obey the same associativity and distributivity properties that their real number counterparts do, so this set of complex numbers is what mathematicians term a ring.
In this system, 
and 
. It can be verified through elementary techniques that all of 
,
, 
, and 
cannot be factored any further in this numbering system - that is to say that all four of these numbers are primes. In our new numbering system, we do not have a guarantee that a given factorization is the only one. A system where we do have such a guarantee is called a unique factorization domain (UFD). So essentially, the fundamental theorem arithmetic asserts that the integers are a UFD.
Show that ,, , and are prime in 
Riemann defined the zeta function for 
real and greater than 1 as :
The zeta function is the sum of the reciprocals of the -powers of the positive integers. The zeta function can be continued analytically across the whole complex plane, except at 
, where it has a simple pole. When people speak of the zeta function, they mean this analytically continued function rather than the summation definition as written above because the most interesting questions are concerned with the complex behavior of this function.
The zeta function is intimately intertwined with the distribution of the prime numbers. For instance, for 
the zeta function can be rewritten as:
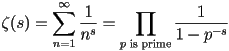
Show that 
for all real 
Hint: use the geometric summation 
along with the fundamental theorem of arithmetic.
The zeta function has trivial zeroes at the negative even integers. The Riemann Hypothesis states that the only other nontrivial zeroes of the zeta function occur on the line of complex numbers where the real part is 
.
One of the most interesting consequences of Riemann hypothesis is that the location of zeroes of the zeta function can be used to bound the error term in the prime number theorem.
Let 
denote the number of prime numbers less than or equal to 
, also called Euler's function. One functional estimate for Euler's function is the following integral:
Here, the 
operator means that the ratio of these two quantities approaches 1 as approaches infinity.
This statement is known as the prime number theorem. We know that asymptotically, these two quantities grow at almost the same rate, but what about how the difference between and 
grows as increases. The quantity 
is known as the error term in the prime number theorem and depends sensitively on the location of zeroes of the zeta function. If all of the zeroes of the zeta function have real part less than or equal to , then
. A refinement of this statement is that if and only if the Riemann Hypothesis is true, then
It is known that all zeroes of the zeta function lie in the critical strip where the real part is between 0 and 1. Several trillion zeroes have been found by computer in this critical strip, and all have real part . Most mathematicians believe that the hypothesis is true.