One interesting consequence of Listing's Law is that whenever a person is looking in a particular direction, the eye is always oriented in the same direction. No matter what path the eye takes to get to a given direction of sight, the image seen will always be the same - there will be no rotation.
Another formulation of his law states that the eye, when moving from looking straight ahead to another direction, then the axis of rotation is the unique line which intersects and is perpendicular to both the initial and final lines of sight. Listing's law is sometimes mistakenly stated as saying that when the eye moves from any sight direction to any other sight direction, the axis that it is rotated on is the unique one that is perpendicular to both the initial and final lines of sight. This formulation cannot be the case because it would imply that the eye can travel a path and end looking the same direction as when it started, except being rotated. We will describe this example in more detail after we've built up the mathematical framework to describe rotations.
Listing's Law was developed by the German mathematician Johann Benedict Listing who lived from 1808 to 1882. Listing worked in a field of mathematics known as
A coffee cup or a donut? Johann Listing can't tell the difference!
Rotations can be described a few different ways in mathematics. Two stand out as being valuable to our present study: a description of the amount of rotation around a named axis and with a matrix. (Another popular and useful way to describe rotations is with Quaternions, but we will not discuss those here.)
The former description of angles rotated around a given line is a fairly straightforward description and has the advantage that it is easy to visualize, but it's drawback is that it is not easy to compose rotations - imagine you have an apple, and you rotate that apple 60 degrees about a vertical axis going through its center of gravity and then you rotate 60 degrees around a horizontal axis through the center of gravity. The composition of those two rotations is again a rotation, so what is its axis of rotation and by how many degrees is the apple rotated? The answer is not easy to come up with, but it is possible to learn the answer through inspection.
Using matrices to describe rotations is less intuitive than describing rotations by their axis, but it makes the job of determining what happens when several rotations are applied to an object almost trivial to compute. To use this method, we will first describe what matrices are and what it means to multiply them together.
What is the matrix?
A 
on the left and 
on the right. Matrices are primarily classified by the number of rows and columns in this rectangular grid, and these numbers are oftentimes called the
A 2x5 matrix: 
A 3x1 matrix: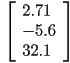 
Writing data in matrix form is a tool used to aid computation. Writing data in the form of matrices never reduces the amount of computation necessary, instead it gives an organization to the data that helps humans keep track of what is going on semantically. Ideally, the organization that a matrix imposes on the data mirrors mirrors the kind of relationships that exist in whatever is being represented. It is up to the writer to ensure that the organization makes sense.
Any matrix with only one column is also called a 
, whose y-coordinate is 
, and whose z-coordinate is 
. The concept of course generalizes to give vectors that describe points in any number of dimensions. The concept of a vector is simply a way to compactly collect all of the information that describes a point in space that is convenient to do computations with, as we will see when we multiply vectors by other transformational matrices.
The way to notate a particular element in a matrix is writing the row and then the column in a subscript, separated by a comma. For example, in the 2x5 matrix:
, would be written:
When counting rows and matrices, start counting at 
instead of with 
, as is the case with most computer science.
Only two matrices with identical dimensions may be added. That is, the two matrices must both have the same number of rows and both have the same number of columns. Matrix addition is done element-wise. That is to say that if 
, 
, and 
are matrices with 
then , , and must have identical dimensions and 
for all valid subscripts 
and 
.
For example:
Matrix addition is associative and commutative. That is to say that for matrices 
,
, and 
with identical dimensions:
Not all combinations of matrices can be multiplied together. Whether or not two given matrices can be multiplied together depends on their dimensions. Specifically, two matrices can be multiplied when the number of columns of the matrix on the left is the same as the number of rows of the matrix on the right. A 3x2 matrix can be multiplied by a 2x5 matrix. However, a 4x5 matrix cannot be multiplied by another 4x5 matrix. This reflects the fact that, semantically, the columns of the left matrix correspond to the rows of the right matrix. The product matrix has the same number of rows as the left multiplicand matrix and the same number of columns as the right multiplicand matrix.
There is a mnemonic trick to remembering these rules concerning dimensions of matrix multiplication. Let us go back to our previous example of a 3x2 matrix being multiplied by a 2x5 matrix. Call the 3x2 matrix and call the 2x5 matrix . The product of these matrices is written as 
or 
. To check if it is valid to multiply these matrices, replace the matrices by their dimensions: 
. The central two numbers here will be equal if and only if it is valid to multiply these two matrices in this particular order. If they are equal, then "cancel" them to get 
, which are the dimensions of the matrix that is the product of the 
matrix by the 
matrix. Remember that this is just a mnemonic trick, and that the "canceling" does not imply anything deeper going on.
Once the dimensions of the product of two matrices are determined, the easiest way to describe the contents of the product of two matrices is to describe how to compute a generic element in the matrix.
Suppose that is an 
-by-
matrix and is an -by-
matrix. We will show how to compute 
, which is an -by- matrix. A generic element of is given by:
One way to visualize this definition is to select a row of the left-hand matrix and a column of the right-hand matrix . Start a the left of the row of and at the top of the column of . Multiply the two terms found in these two locations. Move one entry to the right and one entry down respectively, multiply those entries together, and repeat until you reach the end of the row and column. The fact that the number of columns of is equal to the number of rows in guarantees that the end of the row of will be reached exactly when the end of the column of is reached. It should be clear from this definition why the number of columns of must match the number of rows of 
in order to be able to multiply the matrices.
Matrix multiplication is associative and distributive, but not commutative. That is to say that for matrices ,, and :
The last equation, , is not strictly true. There are pairs of matrices and such that 
, however, these pairs are rare and the exception rather than the rule.
An identity matrix is a square matrix with all zero elements except along the upper-left to lower-right diagonal, all of whose elements are one. There are infinitely many identity matrices, one for each possible dimension. They are all denoted as 
, and the implied context of the dimension differentiates them. The first couple identity matrices are:
and 
in the equation:
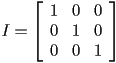
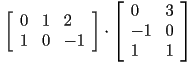
The determinant of a square matrix 
(written 
) is defined as the volume scale factor for the linear transformation associated with . To explicate this a little more, suppose that is a 3x3 matrix, and suppose 
be the linear tranformation from 
to itself associated with , and let 
be any region in 
with a volume of . Then 
is another region in (the region achieved by applying to every point in ), and is defined as being the volume of this region.
For any particular dimension, there is an algebraic formula for the determinant of square matrices in that dimension in terms of the entries in the matrix. For example:
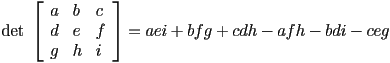
The complexity of the algebraic expressions for the determinant increases exponentially. However there is a recursive definition called Laplace's Formula which is useful for finding determinants of relatively small matrices. For larger matrices, more advanced techniques such as Gaussian Elimination are more efficient. For our purposes, we will only need to find determinants of 3x3 matrices.
Determinants of matrices are multiplicative. That is, if and are square matrices with the same dimensions, then
The transpose of a matrix is a "flipping" of a matrix along the upper-left to lower-right diagonal. The transpose of a matrix is denoted with a small capital "T" written as a superscript to the matrix, such as : 
. To write the definition rigorously, we will show how to compute a generic element in the transpose of a matrix:
For example:
The dimensions of a transpose of a matrix will always be the dimensions of the matrix, but in reverse order.
A linear tranformation is a function from a vector space to another (possibly the same) vector space that obeys the following two properties:
and 
in the domain vector space and scalar values \alpha. The adjective "linear" is often used in mathematics to indicate that addition and scalar multiplication "play nice" with the given object. Here, a transformation between two spaces is called linear when in commutes with both addition and scalar multiplication.
Every matrix corresponds to a linear transformation between finite-dimensional vector spaces with an identified basis, and every linear transformation between finite-dimensional vector spaces with an identified basis corresponds to a matrix. The dimension of the domain of the linear transformation must be the number of columns in the matrix and the dimension of the range of the linear transformation must be the number of rows in the matrix. The transformation that a given matrix corresponds to is the action of left-multiplication on vectors of that space.
For example, let be the 3x2 matrix:
corresponds to a linear transformation from 
, a two-dimensional space, to , a three-dimensional space.
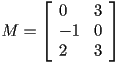
A rotation in three dimensions is a specific kind of linear transformation. The rotation is an action whose domain and range is both , so three-dimensional rotations are all represented by 3x3 matrices. We will only consider rotations which fix the origin. We will show how to identify a matrix as representing a rotation, rather than some other type of linear transformation.
A given matrix represents a rotation if and only if the following two conditions hold:
There are three classes of rotation matrices which stand out because their axis of rotation is one of the coordinate axes.
around the z-axis looks like:
The matrix representing a rotation of 
around the y-axis looks like:
The matrix representing a rotation of around the x-axis looks like:
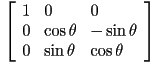
Every three-dimensional rotation is a composition of these three matrices. Can you figure out how?
Every three-dimensional rotation has a single axis of rotation. (The exception to this rule is the trivial rotation, which does not change any point.) Points along the axis are the only points in space which are not moved by the action of the rotation (which is a multiplication by the matrix ). To find these points, first suppose that a generic point 
is on the axis of rotation. This means that the following equation holds:
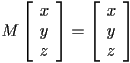
If is a non-trivial rotation, then this equation will always be an under-dertermined linear system of three equations. The solutions to this system will in fact all lie along a line that passes through the origin. If is a solution and 
is a real number, then 
will also be a solution, and vice-versa. This line of solutions through the origin is the axis of rotation for our action induced by the matrix. Though the term is far more general than how it is used here, the vector is called an , and this is a simple way to find the axis of rotation of any three-dimensional rotation.
Suppose that we have an eye in its resting position looking horizontally, and we orient our coordinate axes so that the z-axis points along the direction of sight, the y-axis points up, and the x-axis goes from left to right.