Don and the gang are at it again; this time investiagting the murder of a young girl in a famous Hollywood star's bathtub. As usual, Charlie does his part to help unlock the keys to the mystery. First, he uses Snell's Law (among other things) to identify the victim from a photo. Second, he uses Archemdies' Principle to determine the size of the killer. Finally, he uses some game theory to figure out the motive for the killing.
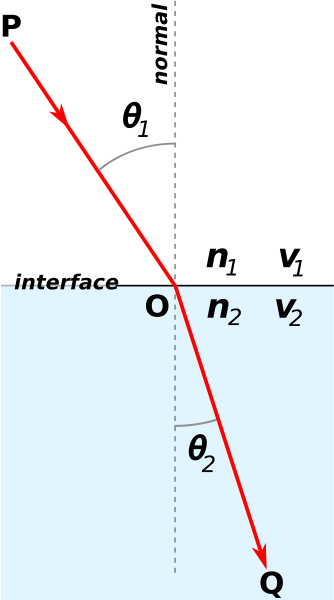
Snell's Law has to do with how light refracts (or bends) when it meets makes the change from passing through air to passing through water (or any other medium).
Let's state Snell's law and see how it applies to our penny/fish situation:

Let's now apply what we have learned to our penny problem:
In the first attempt, we were looking straight down at the penny.
Thus, our angle of incidence was zero. That is, &theta1=0.
Now, since we assume that n1 and n2 are
non-zero, we get that 0= n1sin 0=
n2sin&theta2, and so &theta2=0 as
well. In other words, the light didn't bend at all, and we were able
to touch the penny easily.
When we looked through the side
of the glass however, we got a positive value for &theta1
and thus, the penny looked like it was somewhere it wasn't.
After using Snell's law and facial recognition software to identify the victim, Charlie realizes that he can use some game theory to help determine the motive for the crime. In particular, he uses the concept of risk and response.
A quatifiable way to illustrate this is by thinking about the game of basketball. Consider the great center Shaquille O'Neill. He has made an estonishing 58% of the shots he has taken in his career. However, he has made an abismal 52% of the freethrows that he has attempted. By comparison, Michael Jordan made only 50% of the shots he took in his career but 84% of his freethrows.
Now suppose you have the unenviable task of guarding either of these
to legends. Should you rely on your defence, or foul so that he has
to shoot freethrows? The answer, of course, lies in the math.
If you decide to defend Shaq, he is going to make 58% of his shots.
If you decide instead to foul him when he shoots, the chances that he
hits both freethrows is (.52)2, or 27%. So you clearly run
a much greater risk trying to play defence. Thus, your expected
response would be to foul him. Of course, your strategy chages when
when we add in the rule that you are only allowed to foul him six
times before being removed from the game, but we won't worry about
that for now.
What to do against Michael Jordan, however, is a different story. He
has a (.84)2 or 71% chance of making both freethrows if you
decide to foul him, as opposed to only a 50% chance of making the shot
in the first place. Thus, you risk much more by fouling him than by
defending against him. Let's just hope that your team gets the
rebound the times that he misses!