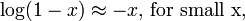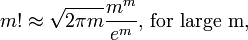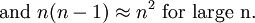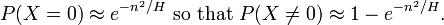Numb3rs 324: The Janus List
In this episode, Charlie has to crack codes. In what follows, we will explain several modern cryptographic methods.
Cryptgraphic Hash function
A hash function takes in a string of characters (usually a string of 0s and 1s) with any length and outputs a string of fixed length. The input is usually referred to as the message. The output is usually referred to as the hash. The hash has fixed length in the sense that every output is exactly the same length. Usually the hashes are viewed as hexadecimal integers.
Hash functions provide a way of determining the fidelity of a password, document, and so forth without having to have the original password or message. For example, computers store passwords as hashes. That way if anyone hacks into the comptuer and discovers the hash corresponding to your password, it doesn't help them steal your identity. However, when you try to log in, you input your password, the computer puts the password into the hash function, and it checks whether the hash saved on the computer and the hash it just computed are the same.
Hash functions should have the following properties:
- It should be hard to invert the hash function. This means that we shouldn't be able to find a rule which undoes the hash so that knowing a hash doesn't help us determine the original message.
- Hash functions are not one-to-one, so, given a particular hash, it should be difficult to construct inputs that have that hash as an output. Even stronger, it should be hard to find construct pairs of messages with the same hash. In other words, hashes should be 'almost unique.'
Hash functions are based upon weaknesses of computers. The algorithms for computing hashes should be rather fast, but only computers from way in the future should be able to determine a message with a particular hash. Since 'way in the future' is of course not a very exact term, new hash functions are being studied all the time to replace old hash functions whose weaknesses have been uncovered. Mathematicians say a hash function is good if it is "computationally infeasible" to do either 1 or 2 listed above.
MD5
MD5, the fifth incarnation of the Message Digest algorithm, is one type of cryptographic hash function.
How it works
The algorithm is relatively simple. Let M be our message of any length.
- First, M is broken up into 512-bit chunks. If the message is not then divisible by 512, the message is appended:
- A single bit, 1, is added to the end of the message.
- Then, as many zeros as are necessary are added until the message is 64 bits shy of being divisible by 512 bits.
- Finally, a 64-bit integer representing the length of the message is appended. In the event that the message is longer than 64-bit, drop all higher order bits until one has a 64-bit integer. Note that the message is now an exact multiple of sixteen 32-bit words.
- A four word buffer (A,B,C,D) is used to compute the hash. Each word is 32-bit, i.e. 8 hexadecimal digits. We initialize as follows:
- A: 01 23 45 67
- B: 89 ab cd ef
- C: fe dc ba 98
- D: 76 54 32 10
- We define the five following operations:
- The binary operation AND. AND takes two binary strings as input (written X AND Y). If in the 2n place of both numbers have a 1, the output has a 1 in the 2n place. Otherwise, put a 0 in the 2n place. Thinking of 1 as true and 0 as false, at each 2n place this operation outputs true exactly when both inputs are true.
- The binary operation OR, written X OR Y. As above except it checks the 2n places of both strings and puts 1 if either of them has a 1 (including the case where both have 1).
- The binary operation XOR, written X XOR Y. As above except it checks the 2n places of both strings and puts a 1 if exactly one of the two strings has a 1 there (but not if both have a 1 there).
- NOT, written NOT X. This takes in a single binary string and replaces every 1 with a 0 and every 0 with a 1.
- The binary operation <<<, written X <<< s. Here X is a binary string and s is an integer. This shifts all the digits of X to the left by s, filling in the holes on the right by zeros and discarding the digits which spill over.
- We now define four functions:
- F(X,Y,Z) = (X AND Y) OR ((NOT X) AND Z)
- G(X,Y,Z) = (X AND Z) OR (Y AND (NOT Z))
- H(X,Y,Z) = X XOR Y XOR Z
- I(X,Y,Z) = Y XOR (X OR (NOT Z))
- Create a function T which takes any of the numbers 1 through 64 as inputs so that T[i] is the integer part of 232 × |sin(i)| where i is thought to be in radians.
- This is a direct quotation of the original memo written by Ron Rivest when he announced the invention of MD5 in 1992. Do the following:
/* Process each 16-word block. */
For i = 0 to N/16-1 do
/* Copy block i into X. */
For j = 0 to 15 do
Set X[j] to M[i*16+j].
end /* of loop on j */
/* Save A as AA, B as BB, C as CC, and D as DD. */
AA = A
BB = B
CC = C
DD = D
/* Round 1. */
/* Let [abcd k s i] denote the operation
a = b + ((a + F(b,c,d) + X[k] + T[i]) <<< s). */
/* Do the following 16 operations. */
[ABCD 0 7 1] [DABC 1 12 2] [CDAB 2 17 3] [BCDA 3 22 4]
[ABCD 4 7 5] [DABC 5 12 6] [CDAB 6 17 7] [BCDA 7 22 8]
[ABCD 8 7 9] [DABC 9 12 10] [CDAB 10 17 11] [BCDA 11 22 12]
[ABCD 12 7 13] [DABC 13 12 14] [CDAB 14 17 15] [BCDA 15 22 16]
/* Round 2. */
/* Let [abcd k s i] denote the operation
a = b + ((a + G(b,c,d) + X[k] + T[i]) <<< s). */
/* Do the following 16 operations. */
[ABCD 1 5 17] [DABC 6 9 18] [CDAB 11 14 19] [BCDA 0 20 20]
[ABCD 5 5 21] [DABC 10 9 22] [CDAB 15 14 23] [BCDA 4 20 24]
[ABCD 9 5 25] [DABC 14 9 26] [CDAB 3 14 27] [BCDA 8 20 28]
[ABCD 13 5 29] [DABC 2 9 30] [CDAB 7 14 31] [BCDA 12 20 32]
/* Round 3. */
/* Let [abcd k s t] denote the operation
a = b + ((a + H(b,c,d) + X[k] + T[i]) <<< s). */
/* Do the following 16 operations. */
[ABCD 5 4 33] [DABC 8 11 34] [CDAB 11 16 35] [BCDA 14 23 36]
[ABCD 1 4 37] [DABC 4 11 38] [CDAB 7 16 39] [BCDA 10 23 40]
[ABCD 13 4 41] [DABC 0 11 42] [CDAB 3 16 43] [BCDA 6 23 44]
[ABCD 9 4 45] [DABC 12 11 46] [CDAB 15 16 47] [BCDA 2 23 48]
/* Round 4. */
/* Let [abcd k s t] denote the operation
a = b + ((a + I(b,c,d) + X[k] + T[i]) <<< s). */
/* Do the following 16 operations. */
[ABCD 0 6 49] [DABC 7 10 50] [CDAB 14 15 51] [BCDA 5 21 52]
[ABCD 12 6 53] [DABC 3 10 54] [CDAB 10 15 55] [BCDA 1 21 56]
[ABCD 8 6 57] [DABC 15 10 58] [CDAB 6 15 59] [BCDA 13 21 60]
[ABCD 4 6 61] [DABC 11 10 62] [CDAB 2 15 63] [BCDA 9 21 64]
/* Then perform the following additions. (That is increment each
of the four registers by the value it had before this block
was started.) */
A = A + AA
B = B + BB
C = C + CC
D = D + DD
end /* of loop on i */
- With the new A,B,C, and D defined above, apply this to the next 16-word block, and so forth, until all the blocks have been done.
- The algorithm finally outputs a string ABCD (where we are just concatenating the strings).
- One should note that the 32-bit strings A,B,C, and D are treated slightly differently. The string 01 23 45 67 is treated by the algorithm as the hexadecimal number 67452301 (each 2 digit pair is in order, but the pairs are reversed). Likewise, the output is the concatenation of A,B,C, and D in this new ordering.
Even slight changes in the initial input will, with near-absolute certainty, produce completely distinct hashes. When transmitting a document over the internet, only small errors are likely to occur, so this feature of MD5 makes it quite good in determining if a document has been corrupted in transit. For cryptographic applications, MD5 was found to suffer from a number of weaknesses.
Why it doesn't work that well for encryption
One major fault of MD5 encryption is the relative ease in constructing collisions. A collision occurs when two inputs produce the same hash output. Rather than having to crack the encryption, one can implement a a so-called birthday attack - named after the birthday paradox from mathematics. The birthday paradox comes from the following:
Activity 1:
Assume that birthdays are equally distributed among all 365 days (of course we are not allowing a leap year here either). Find a formula for the probability that at least two people in a group of n people have the same birthday. What is the number n required to put that probability at above 50%?
The answer to the above problem generally defies our intuition - it is much smaller than we may think at first - which is why we call it a paradox.
So what does this have to do with collisions? Well, consider the following computation. Suppose that there are H possible hashes. Out of these H possible hashes, we pick n of them. Every time we pick, each possible hash is equally likely to be picked, i.e. is picked with probability 1/H. Let X denote the number of collisions after picking n hashes at random. What is the probability that X = 0? Well, we have H choices for the first selection, then H-1 for the second, H-2 for the third,..., and H-n for the nth. Hence we get that

Activity 2:
Suppose that H is much larger than n and that n is much larger than 1. Assume the following facts:
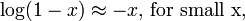
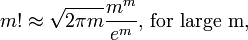
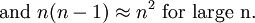
Show then that
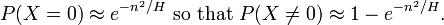
For further review, the first fact comes from the Taylor expansion of the log function. The second fact is known as Stirling's Approximation. The last fact is just pretty obvious.
Once we have the above, we can solve for n, and obtain (letting p = P(X > 0))
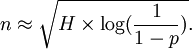 Thus if we want to know the number of times we should pick at random to get a collision 50% of the time, we would plug in p = 0.5 and the above would give us about how many we should pick.
Thus if we want to know the number of times we should pick at random to get a collision 50% of the time, we would plug in p = 0.5 and the above would give us about how many we should pick.
The MD5 algorithm outputs a 128-bit number, so that there are about 3.4 × 1038 unique hashes. So to get a collision 50% of the time, we would need to randomly select about 1019 different hashes. As of 2007 the time required by the world's fastest super computers to perform this task is on the order of days. However, since this is a brute force tactic - any powerful brute of a computer could do this without any ingenuity - a targeted algorithm can complete this task much, much faster. In fact, in 2006 Vlastimil Klima wrote an algorithm that can produce a collision using a desktop computer in under a minute. As computing power rapidly increases, the production of rainbow tables (described below) will make the MD5 hash function completely obsolete. One should observe, though, that the birthday attack is, for now, only effective against short hashes - even a 256-bit hash would render such an attack useless for 2008 computers.
SHA-1
SHA-1 is the second incarnation of the Secure Hash Algorithm. It is currently one of the Secure Hash Standards of the United States (as set by the National Institute of Standards and Technology). However, several weaknesses have been determined. SHA-1 has three revisions, SHA-256, SHA-384, and SHA-512. These four are the official Secure Hash Standards of the USA.
These four algorithms work much in the same way as MD5. They begin by padding the message, i.e. increasing it's length to be a multiple of some number. They then parse the padded message, i.e. breaking it into distinct pieces. A set of initial hash values is prescribed. An algorithm then runs through the first chunk of the padded message and updates this hash, then applies the algorithm to the second chunk of the message, updates the hash, and so forth. The NIST FIPS 180-2 document published by the National Institute of Standards and Technology outlines the exact workings of each SHA algorithm.
Rainbow Table
A rainbow table is a lookup table - a kind dictionary - of hashes. That is to say that it is esssentially a compiled list of hashes together with a string which produces that particular hash. Often there is a simplifying algorithm used to reduce the amount of physical storage space required to store the tables, although this increases the time required to translate a particular hash into its encoded message. It is an inefficient - but often effective - method to attack secured computer systems. If a list of hashed passwords is procured from a secure system, the rainbow table can be used to produce passwords which match those hashes exactly.
How to Defeat Rainbow Tables:
Good encryption systems are protected against rainbow tables. One easy way to provide such protection is to simply increase the length of all encoded messages by adding a string to the end of every message. This added string is called a salt. This increases the storage space required by a rainbow table because the effective length of the passwords is increased by the length of the salt. Using fixed string is relatively weak. If a hacker figures out that string somehow, everything is for naught. Often it is better to have an algorithm which adds to the end of every message some string which is user-specific.
Windows
Constructing a rainbow table might seem like a stupid trick, but they have proved to be surprisingly practical. For example, Microsoft Windows 2000 and XP use a very weak form of password encryption. Each password is broken up into blocks of seven characters, then hashed. This is weak because, regardless of length, each password is really only as strong as a seven character password. The rainbow table needs only construct include all passwords of length 7, or about (80)7 passwords. Even a desktop computer can produce such a table in a short period of time.
Classic Encryption Systems
Charlie also encounters a number of classic examples from cryptography. You can find more about them at
- Merkle Hellman Encryption
- Straddling Checkerboard Cipher
- Substitution Cipher
- Bacon's Cipher
- Knapsack Cipher
Wheat and Chessboard Problem
At the beginning of the episode, Charlie is asked a series of questions. One is how many pieces of wheat would be placed on a chessboard if one placed 1 piece on the first square, 2 on the second square, 4 on the third square, 8 on the fourth square, and so forth. The answer is relatively simple. There are 64 squares on a standard chessboard, so the number S of pieces of wheat is given by S = 1 + 2 + 4 + 8 + ... + 261 + 262 + 263. Using the fact that 2x - x = x, it is easy to see that S can be written more compactly: S = 264 - 1. Charlie actually says the wrong number. He says seven-hundred ninety-nine million. It is actually seven-hundred and nine million.