Numb3rs 215: Running Man
In this episode several different mathematical topics are mentioned, but we're
going to focus on LIGO and Benford's law.
Laser Interferometer Gravitational-Wave Observatory
LIGO is the place where the fictional character Larry works, but it is also
a scientific project in real life. It is a joint project by Caltech and MIT
which is designed to detect gravitational waves. These can be understood by
analogy to waves in a pond. (Look
here
for more information about waves.) Imagine a very still pond on a windless
day. The
top of pond will be completely flat. We can describe this mathematically by
assigning each point of the pond a number H(x,y,t) corresponding to its
height, and in this case, each point in the pond has the same height. This is
described by the equation H(x,y,t) = c, where c is
a constant. Now if a rock is dropped into the middle of the pond, the
function H(x,y,t) will no longer be a constant, but will vary as
a function of time t and position x,y.
The function in general is difficult to
describe because it depends on the boundary of the pond as well as how you
choose to model dropping the rock, but if you fix the position and just
look at the height of one point as a function of time, (i.e.
f(t) = H(x,y,t)), then you get something like f(t) =
cos(t).
Now to understand gravitational waves, we have to describe gravity in a way
similar to our description of the height of the pond. To do this, we have
a function G(x,y,z,t) which to each point in space x,y,z and
time t assigns some kind of mathematical object to describe the
gravity. Let's think for a bit about what we need to describe gravity.
We can feel a force from gravity, and the strength (or magnitude)
of that force depends
on where we are. However, the direction of that force also varies depending
on where we are. A mathematical object which describes a direction and
magnitude is called a
vector, so our function G must assign a vector
to each point in space and time.
Actually, if you're careful you'll realize that at any point on the Earth
the gravitational force isn't a constant as a function of time, even without
gravitational waves. Do you know why? A partial answer is that the moon exerts
a gravitational force on the earth that changes as the earth
rotates. This is the main cause of the
tides in the ocean.
Now the goal of LIGO is to detect such waves. The basic idea of how this
is done is as follows. The scientists built two mile-long tubes that are
perpendicular to each other. Then a laser beam is split so that it travels
down each othe tubes at exactly the same time. At the end of each tube are
mirrors that reflect the beam back to its starting point. The tubes
are built with very precise lengths so that if there are no gravitational
waves, then the two beams are exactly out of phase so they cancel out (this
means that if you write the equation for the intensity of the two beams
at the point where they meet, they look something like cos(t) and
cos(t + &pi ), so when they add together you get 0, which means there's
no laser light). However, if there
is a gravitational wave that is oriented in the right direction, it will change
the length of one of the tubes but not the length of the other, and this
will make it so that the two beams aren't out of phase anymore. This means
there will be a brief flash of light where the two beams meet.
Benford's Law
In this episode then mention Benford's Law, and even though they don't
actually use it in the show, it is an interesting law that deserves some
explanation. Benford originally published a paper describing this pattern
in 1938. The inspiration of this paper was his observation that in books
that had dozens of pages of logarithm tables the pages of the table of
numbers that started with 1 were more worn than any of the other pages.
(Before computers were invented, people
computed things by hand, and logarithms can be used for several different
shortcuts, so books containing many pages of tables of logarithms were
commonly used.) Benford gathered numbers from many different sources and
counted the number of numbers starting with each digit. As an example,
he gathered the area of 335 rivers and came up with the following counts.
(The full table from his paper can be found here.)
| 1 | 2 | 3 | 4 | 5 | 6 |
7 | 8 | 9 |
| Area of Rivers |
31.0 |
16.4 |
10.7 |
11.3 |
7.2 |
8.6 |
5.5 |
4.2 |
5.1 |
Activity 1:
Pick some quantity, like areas of lakes, population, lengths of
books, or anything you like, and gather a large number of measurements
of this quantity (ideally between 50 and 100). Then count the number
of measurements that start with each digit and make a table similar to the
one above.
There is a simple intuitive explanation for this phenomenan. Many
quantities in nature satisfy the property that is the quantity changes
randomly, the amount of the change is likely to be proportional to quantity.
Another way to say this is that if q is the quantity that changes
randomly, it is likely to fall into the range .9*q to 1.1*q.
Then if q starts with a large digit, like an 8, it is much more likely
to change to a number that starts with a different digit than it would be
if q started with a 1.
Let's give a more precise mathematical explanation. The above paragraph
states that many quantities that arise in nature can be modelled as
a product of a large number of random numbers between .9 and 1.1.
Then we have the equations and .
Here each
is a random number between .9 and 1.1.
We don't know what the actual distribution between .9 and 1.1 is, but
as long as we assume it's nice enough, it turns out that it doesn't matter.
Let's diverge just a little bit to talk about the
Central Limit Theorem.
The statement of the theorem is that the sum of many independent and
identically-distributed random variables is well approximated by a normal
distribution. To understand this, first we'll do an example, and then
we'll apply the statement to the example.
Activity 2:
- If you roll a fair dice, draw a graph of the probability that
each of the numbers come up. (i.e. the x-axis of the graph should be the
numbers 1,2,3,4,5,6, and the values above
these numbers should be the probability that they occur.)
- Now draw a similar graph for the probabilites of getting the numbers
2 through 12 if you roll two fair dice at once.
- Now draw a similar graph for rolling three dice at once.
- What patterns do you notice?
In this example, the random variable is each dice. The random variables are
independent because the way one dice lands doesn't affect the way another
dice lands, and they are identically distributed because all the dice are
the same. The normal distribution is a particular probability distribution,
also called the Gaussian distribution or Bell curve. A picture of
several different normal distributions can be found
here, and a description of the distribution is
here. You
should notice the similarity between these pictures and the later graphs
you drew in the activity. The basic idea is that if you add up a lot
of random events to get a number, that number will have a distribution
that looks like a Bell curve.
Now we can apply this to our situation to conclude that the distribution
for log(q) will look like a Bell curve. Now how is the
first digit of q is related to log(q)? If we are taking
all the logarithms using base 10, then since  ,
we can let a be the integer part of log(q) and b
be the decimal part. Then the first digit of q only depends on
b. Now to figure out the distribution of the first digit of
q, all we need to do is figure out the distribution of b.
To do this, we break up the graph of the distribution of log(q),
(which is similar to a Bell curve) up into slices that have width 1 and then
take the average of all these. If the Bell curve is very wide (which
corresponds to q having a large range of possible values), then
since the Bell curve is symmetric, the distribution of b should be
close to flat, so b has an almost equal chance of being any number
between 0 and 1. Now if
,
we can let a be the integer part of log(q) and b
be the decimal part. Then the first digit of q only depends on
b. Now to figure out the distribution of the first digit of
q, all we need to do is figure out the distribution of b.
To do this, we break up the graph of the distribution of log(q),
(which is similar to a Bell curve) up into slices that have width 1 and then
take the average of all these. If the Bell curve is very wide (which
corresponds to q having a large range of possible values), then
since the Bell curve is symmetric, the distribution of b should be
close to flat, so b has an almost equal chance of being any number
between 0 and 1. Now if 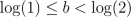 , then the first digit of
, then the first digit of
 will be a 1, which leads to the formula
will be a 1, which leads to the formula

Let's test our predictions. We can do this by generating a random number
q and then multiplying it by R random numbers  each of which ranges from .9 to 1.1. We'll do this N times and then
record the results in the table below.
each of which ranges from .9 to 1.1. We'll do this N times and then
record the results in the table below.
Activity 3: You can modify N, the number of
trials to run, and R, the number of random numbers to multiply together,
and then run the calculation again. Try to figure out what values of N and
R make our predictions accurate. To limit the computation time, N must
be less than 1500 and R must be less than 2000. The computation might
take a few seconds.
| Starting digit: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Count: | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Percentage: | |
 ,
we can let a be the integer part of log(q) and b
be the decimal part. Then the first digit of q only depends on
b. Now to figure out the distribution of the first digit of
q, all we need to do is figure out the distribution of b.
To do this, we break up the graph of the distribution of log(q),
(which is similar to a Bell curve) up into slices that have width 1 and then
take the average of all these. If the Bell curve is very wide (which
corresponds to q having a large range of possible values), then
since the Bell curve is symmetric, the distribution of b should be
close to flat, so b has an almost equal chance of being any number
between 0 and 1. Now if
,
we can let a be the integer part of log(q) and b
be the decimal part. Then the first digit of q only depends on
b. Now to figure out the distribution of the first digit of
q, all we need to do is figure out the distribution of b.
To do this, we break up the graph of the distribution of log(q),
(which is similar to a Bell curve) up into slices that have width 1 and then
take the average of all these. If the Bell curve is very wide (which
corresponds to q having a large range of possible values), then
since the Bell curve is symmetric, the distribution of b should be
close to flat, so b has an almost equal chance of being any number
between 0 and 1. Now if 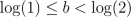 , then the first digit of
, then the first digit of
 will be a 1, which leads to the formula
will be a 1, which leads to the formula

 each of which ranges from .9 to 1.1. We'll do this N times and then
record the results in the table below.
each of which ranges from .9 to 1.1. We'll do this N times and then
record the results in the table below.