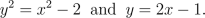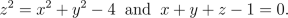Numb3rs 313: Finders Keepers
The FBI puts Charlie on the case of figuring out the path of a downed marine salvage barge - as Don strongly suspects that the death of its crew wasn't an accident. The marine salvage barge was trying to locate the remains of a yacht, traveling on an around-the-world race and with millions of dollars of design invested in it - and under maritime laws, the property of whoever finds it first! At the same time, the NSA demands his assistance in finding the yacht for reasons of their own.
How would Charlie even know where to begin in looking for the yacht or the downed salvage barge? Although there are complications involved in tracking ocean current influences, this problem can be simple enough to solve ourselves!
For starters, most of these questions involve optimization and constraint - asking the questions "where can we reach from point A with X amount of fuel" or "what obstacles do we need to go around or take into account?"
A First Example:

Say you're leaving the shoreline (a straight, long beach) at a fixed point, with 100 gallons of fuel. If you can travel 2 miles to the gallon in still waters, what's the furthest you can go?
This question so far is really easy. Clearly, we can go up to 200 miles from the shore. As we can't take our boat back on the land, the limits of where we can go trace out of semi-circle on the water ahead of us.
More Realistic Example:
As some of you might have noticed, this isn't all that likely a scenario. Boats can move faster (and use less gas) with the current, and slower (and use more gas) against the current. If we have a current flowing straight to the right of 5 miles per hour, what does our new range look like?
We can't solve this the way we did before. Previously, our velocity didn't matter (we could assume that it was constant) and we didn't need to keep track of the direction we were traveling relative to a current. Now we need to know how LONG our boat can travel for, and instead of measuring just miles traveled before we run out of gas!
Let's say the boat travels about 25 miles per hour, and we still get about 2 miles per gallon. Let's work through this slightly harder example as an activity.
Activity 1:

- How long does it take before we run out of fuel? (This will be our final time T.)
- What's the furthest you think the boat can go to the left? How about to the right? What about if the boat heads out straight perpendicular to the shore (and doesn't fight the current)? If you're propelling the boat straight away from the shore but not fighting the current, where would you end up and why?
- To figure this out exactly, we're gonna need to be a little more rigorous. The easiest way to do this is to assume that wherever the boat would be at time T if it's heading off straight (in some direction) is going to just be it's original position in (x,y) plus (2T,0). Explain why this makes sense.
- From trigonometry, if we head off at angle THETA (and always keep our engine pointed in the same direction), what (x,y) do we end up at at time T? [Note that the angle between the shore and our boat isn't going to be the same THETA as the direction our engine is pointed in!]
Other Optimization Problems:
Let's consider some other optimization problems. So far, we've just been looking at figuring out how far you can travel with a fixed amount of fuel in some direction. What other optimization problems come up? Well, a lot of algebra and calculus are devoted to those questions!
Activity 2:
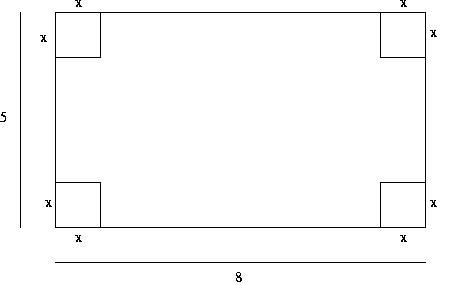
Say you want to construct a box from a piece of cardboard 5 inches by 8 inches. If we cut squares of size x from each of the corners, what's the largest volume box we can make? Let's break this down into steps.
- What is the formula for the volume of the box with the corners cut out?
- Graph this using your calculator.
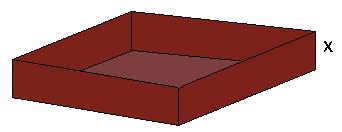
- To maximize this, we take the derivative of this formula with respect to x, then look for zeros of this new function.
Real Life Applications
These problems really do come up all the time in real life. In metal and plastic fabrication, car and space shuttle design, economic planning strategies, orbit trajectory calculations, bridge and building construction, and many, many other diverse areas in manufacture and planning.
In other directions, discrete optimization arises in planning minimal paths for "traveling salesman" type problems, network design and flow analysis, construction of cell phone towers, public infrastructure, etc. Instead of using calculus to produce answers for these, often complication graph theory will wind up getting used. To read a little more about this direction, check out this
site and this
link..
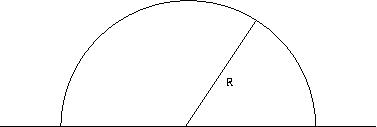
Activity 3: Let's say we want to make a window with a rectangular mid-section, and a semi-circle for the top. If we only have 10 feet of building material for a frame, what's the window with the most view of the outside we can make?
- Write the formula for window area in terms of just R.
- Graph this using your calculator.
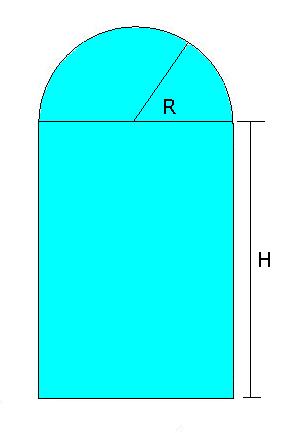
- Maximize your window area.
Let's do one more optimization activity. This'll be optimization subject to constraint - namely, we'll want to figure out what point is farthest from the origin that lies on both a parabolic surface and a plane intersecting that sphere. We'll do the easy (2-dimensional) version of this first, then try the 3-dimensional version next!
Activity 4: Let's take a parabola and a line given by the following equations:
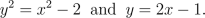
- Graph these equations.
- How many points are there that are on both the parabola and the line? Calculate which of the points is closer.
Activity 5: Now let's try this again for the 3-dimensional case.
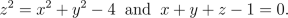
- Consider the graph below. How many points are there that are on both the parabolic surface and the plane? Why is this problem harder?

- Write out an equation for the intersection of the parabola and the plane in terms of just x and y. If we project this curve down onto the (x,y)-plane, calculate the point furthest from (0,0).
- Now in 3-space, calculate the point furthest from the origin (0,0,0).
 Let's consider some other optimization problems. So far, we've just been looking at figuring out how far you can travel with a fixed amount of fuel in some direction. What other optimization problems come up? Well, a lot of algebra and calculus are devoted to those questions!
Let's consider some other optimization problems. So far, we've just been looking at figuring out how far you can travel with a fixed amount of fuel in some direction. What other optimization problems come up? Well, a lot of algebra and calculus are devoted to those questions!