Numb3rs 209: Toxin

After four people nearly die from poisoning, Don learns someone is tampering with nonprescription drugs. When the perpetrator publishes a manifesto in a local paper, Don is led to believe the person may be a former employee of the drug company that manufactured the drug.

In this episode, Charlie uses information theory and information entropy to help understand the manifesto and probabilistic graph theory in an attempt to determine where the perpetrator is likely to be found.

How do you measure information?

Charlie describes Information Theory as the branch of mathematics that formalizes the study of how to ``get a message from point A to point B'' and explains that this theory provides a good working definition of what the information content of a message is. As there are different ways to hear the same song for example, this definition should not depend on the form of the message.

A very common mistake is to believe that information theory is about what messages mean, that is to say to believe that content means here quality rather than quantity.

Indeed, tools like information entropy allow mathematicians to give meaning to and answer sentences like ``how much information is present in this message'', just like a scale tells you how much something weighs without saying anything about whether it's steel or wood, for example.

Information theory is generally considered to have been founded in 1948 by Claude Shannon in his seminal work, A Mathematical Theory of Communication. The central paradigm of classical information theory is the engineering problem of the transmission of information over a noisy channel.
Applications of fundamental topics of information theory include lossless data compression (e.g. ZIP files), lossy data compression (e.g. MP3s), and channel coding (e.g. for DSL lines). The field is at the crossroads of mathematics, statistics, computer science, physics, neurobiology, and electrical engineering. Its impact has been crucial to success of the Voyager missions to deep space, the invention of the CD, the feasibility of mobile phones, the development of the Internet, the study of linguistics and of human perception, the understanding of black holes, and numerous other fields (Wikipedia, read more about this here).

Information Entropy

Suppose you were to ask someone you just met for them to tell you their address. From a mathematical point of view, this experience is similar to randomly picking an address out of the yellow pages, say. Indeed, while you can't tell a priori what the answer is going to be, different locations are more or less likely depending on the context - the languages they speak, for example, or whether they go to your college.

Another important concept in information theory is that of noise, which generalizes the intuitive definition of that word. For example, a very loud car passing by could make you misshear the person you're talking to and alter the message that you get, as electromagnetic interferences could modify the signal your cell phone is picking up.

We are thus led to model the process of ``getting a message from A to B'' as a random process. In other words, receiving a message becomes sampling a random variable.

Suppose now given a question X whose possible answers are x1,...,xn, and assume that the probabilty that the answer that you actually get be xi is pi. Thus by definition P(X = xi) = pi.

We would like to assign to this question X a numerial value - i.e. a number - H(X) called its entropy and measuring ``how much information you would get if you knew the answer to X''. How to define such a function is not obvious, at first sight. The following activity explores the first properties one would expect H(X) to satisfy if it indeed existed.

Activity 1 Which one of the following messages do you think provides "more information" -- i.e. should have a higher entropy?
  1. The result of fair tossing a coin
  2. The result of tossing a coin that falls on heads 99% of the time
What if X is such that p1 = 1 and the other pi's are all zero? What should H(X) be? In other words, if you already know your favorite band is playing this weekend, and one of your friends tells you they're playing this weekend, then this is as if they hadn't told you anything -- information theory-wise, that is.

Now, suppose you have two questions X and Y, how much information is contained in knowing the answer to both X and Y? We know the information given by X is H(X) and that given by Y is H(Y), so you might be tempted to think the answer is H(X) + H(Y). Indeed, if you're given one pound of apples and one pound of oranges, you do have two pounds of fruits. One has to be more careful here, though. If X and Y are not inpendant (if X = Y for example) then the above additive formula can't hold. In other words, knowing one person's name and their name doesn't count as knowing two things about that person, obviously!!


The concept of entropy was originally a thermodynamic one which has then been adapted to other fields of study, including information theory, psychodynamics, thermoeconomics, and evolution. The statistical definition of entropy, which describes it as the number of possible microscopic configurations of a macroscopic system, is the more fundamental definition and all other definitions and properties follow from it, including the definition used here.

Other mathematical considerations show that there is a function H that satisfies all these properties and whose definition is the following:

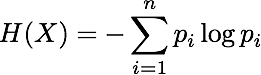
Definition For a discrete random variable X that can take values x1, ...,xn with probability pi respectively, define the entropy H(X) of X to be
Then H(X) provides a good measure of the "quantity of information" provided by the message X.

The following activity should help you convince yourself that this is a reasonable definition

Activity 2 Suppose X is a random variable that takes values '0' and '1', with probability p and (1-p) respectively. Write H(p) for H(X).
  1. What is H(1)? H(0)? What about H(0.99)? Is this compatible with what we were expecting in activity 1?
  2. When is H(p) maximal? Try to solve for p in H'(p) = 0
This last fact is in fact general. Say X can now take values x1, ..., xn with probability pi respectively. Find the values of pi that make H(X) maximal. Here again, you can start by looking at grad H = 0 as a function of the pi's.

The following activity is more challenging and involves calculating the entropy of a non-trivial random process:

Activity 3 A tennis match has several sets. In a "best of five" game, the player that wins three sets is the match winner. It is assumed that it is equally probable for both players to win a set and the sets are played independent from each other. Let X be the random variable that represents the series of set winners. Possible values of X are X = AAA or X = BABAB, for example. The random variable Y denotes the winner of the game, thus in the two previous examples, Y would take the values Y = A and Y = B rexpectively.
  1. What is the entropy H (X) of the series of set winners?
  2. What is the entropy H (Y) of the winner variable?
  3. The probabilities of winning a set are now different. Let p denote the probability that player A wins a set. What is the probability p that maximizes the entropy H (X) and H (Y)?
  4. What is the probability p that minimizes H (X) and H (Y)?
  5. What are the entropies H (X) and H (Y), if player A wins every set?
You can have a look at the tree desribing all possible events here.

What do you measure information in?

Now that we have defined the entropy of a random variable and said that it measures the "information content" of a message, the only thing missing is a unit.

So what unit do we measure entropy in? From now on, we'll assume the logarithm in the definition of entropy is taken to be the base-2 logarithm log2, defined by log2(x) = log(x) / log(2).

Activity 4: Towards bits
  1. As a warm-up, what is log2(2n) ?
  2. Suppose we're interested in sending one character among 2n possible ones, all equally likely. What is the entropy of such a message?
  3. Suppose now that you are given a panel of toggle switches lined up in a row. Suppose there are m switches. We would like to assign to each configuration of the switches one of the values the message can take. How many messages can you encode with m switches? How many switches does it take to encode 3 possibles messages? 54 messages?
  4. Suppose now we are sending a string of 0's, each 0 being one message. What is the entropy of such a message?

Knowing whether a switch is on the on or off position is the most elementary piece of knowledge -- as is any answer to a yes or no question. It can be encoded with an alphabet of two caracters, 0 (for off) and 1 (for on) for example. We call such an information a bit.

We have seen that it takes n bits, that is to say n switches if you will, to encode the value of a message that can take 2n equally likely values. We have also seen that the entropy of such a message is exactly n.

On the other hand, if we already know the message, there is no need for any bits to encode the information, and the entropy is also 0.

This suggests that entropy might be a measure of how many bits are needed to encode the value of a message. Further investigations show that this is indeed true, as long as one considers this number of bits as a theoretical lower bound -- meaning you would need at least that many bits.

Important fact The entropy of a discrete random variable provides a theoretical lower bound on how many bits are needed to encode samples of that variables.

In other words, entropy measures the content of a message in bits

Compression: Towards the theoretical bound

The following activity introduces the notion of data compression and shows how one can get closer to the theoretical bound provided by the entropy.

Activity 5: Towards the bound, data compression

Suppose we are investigating sending a one character message that can take values amongst a, b, c or d with probabilities given in the following table:

xiabcd
pi2/34/274/271/27
  1. What is the entropy of such a message?
  2. How many bits are actually needed to assign to each combination one of the values a, b, c or d?
  3. Suppose we use the following association:
    xiabcd
    Bits00011011

    We want to encode the following sequences of messages: aaabaccbaa and abacaaaaaa. How many bits are needed to encode those sequences? What are the corresponding bit sequences?

  4. Suppose now we use a different association. We want the most frequent messages to be encoded with the least number of bits, while the less frequent ones can take more. Consider the following association:
    xiabcd
    Bits010110111

    What are now the bit sequences corresponding to our previous two sequences (aaabaccbaa and abacaaaa)? How many bits are actually used needed now? What is the average number of bits per message, that is to say per character? How does this relate to the entropy you calculated in question 1?

    5. What happens now if you are given a sequence of bits, that is to say a sequence of 0's and 1's? Is it always an actual sequence of a's and b's that has been encoded using the technique in question 3? If so, can you decode it? In other words, do you always know how many bits need to be read in a row at a time?

    the following decision tree might help you amswer those questions.


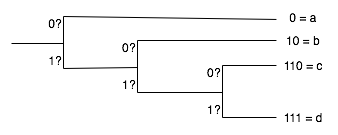
So how does one go about constructing such trees? The example above is in fact a very example of what is called data compression and the idea used to construct the above table is based on the same kind of ideas the ZIP compression technique is. To learn more about this, you can read this.