Numb3rs 210: Bones of Contention

A young woman working at the Museum of Natural History near CalSci is murdered, leaving behind only a few cryptic equations in a notebook. After Charlie examines the notebook, he realizes that the equations date a new find to 10'000 years old -- a human skull that would be the oldest remains ever found in the area, predating the existing Native American tribe in place by thousands of years.

How do equations combine with the properties Carbon 14 to allow scentists to do Carbon dating?

Carbon Dating

Carbon 14, also written 14C is a radioactive isotope of carbon that is produced in the upper atmosphere by radiation from the sun: neutrons hit nitrogen-14 atoms and transmute them to carbon.

Trees, flowers and other land plants get the carbon they need to activate the photosynthesis process from carbon dioxide in the air. Some fraction of their carbon is thus 14C, and hence the same is true of all the creatures that get their carbon by eating such plants, or by eating creatures that eat seach plants, and so on. Living organisms remain in a state of equilirium with their environment and hence hold a somewhat predictable quantity of radioactive carbon.

Suppose now that such an organism dies and its body is preserved. The radioactive carbon in its body will undergo radioactive decay and gradually turn back into Nitrogen. Luckily for us, this process is regular enough that we can model its evolution with mathematical equations.

Activity 1 Carbon decays with a half life of (about) 5730 years. This means that if we start with a certain amount of radioactive carbon in a sample, exactly half of it will have decayed after 5730 years. Assume we start with a sample containing 1000 atoms of radioactive carbon.
  1. How many years will it take to have 500 atoms left? 250 atoms left?
  2. Can you generalize that to numbers of the form (1/2)n 1000?
  3. Suppose we are dating a sample that we know originally contained 1000 radiocative atoms but that now only contains 360 left. Can you tell how old the sample is? Can you give an exact answer or just an estimate? How about 20 atoms left?
  4. How old do you think a sample has to be before this type of dating is no longer useful?

When trying to calculate the age of the sample containing 360 radioactive atoms, you should have noticed that you could only give an approximate age. To try and understand why, we will first simplify the problems a little a bit by choosing different units of atoms and time

Let us thus assume that the number N of atoms is 1 unit at t = 0, and that after 1 unit of time, only one half units remain in the sample. Using carbon dating vocabulary, this says that the half life is now 1 unit of time. We'll try and investigate the value of N(t = 1/2) :

We know that as time passes from t = 0 to t = 1/2, the number N of radioactive atoms gets multiplied by some factor mu1, and that as time passes from t = 1/2 to t = 1, that number gets multiplied by some other factor mu2. But we also know that after one period of time, N is divided by 2.

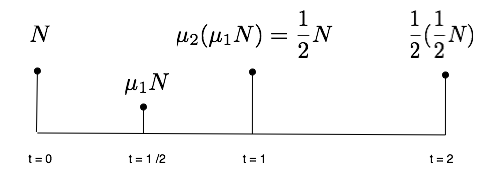
So as long as mu1 mu2 = 1/2, these two numbers can be anything and are not directly specified by the model, at first sight.

This is where we make a choice as mathematicians modeling this problem.

We know that the factor that takes N from t = 0 to t = 1 is the same as that which takes N from t = 1 to t = 2. If we want our model to make sense, it should respect this symmetry and we should have mu1 = mu2 = mu, and thus the following equations:

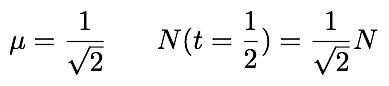
We now apply this knowledge to our original example:

Activity 2 Assume the sample starts with 1000 radioactive carbon atoms.
  1. How many atoms left are there after 2865 years?
  2. Can you calculate how many atoms are left after 1910 years?
To find the answer to the last question, you are going to need to use a diagram similar to the one we used to derive the value of N(t = 1/2), but this time, split the time period as follows:

Exponential Decay: A Functional Equation

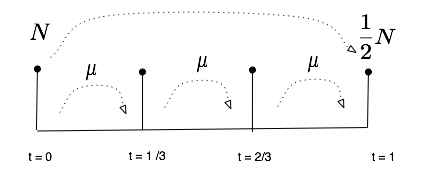
In this section, we investigate what is called a functional equation, that is to say an equation where the unknown is a function and not just a number. Assume here again that the half life is one unit of time, and call N(t) the number of units of atoms in the sample at time t. We will write an equation for N as a function and try to investigate some of its solutions.

Activity 3
  1. Write an equation relating N(t) and N(t+1), that is to say, the amount of radioactive atoms at some time t and after exaclty one half life. This is called a functional equation as the unknown is the function N itself.
  2. We already know one function that satisfies this equation N(t) = (1/2)t. Check that it is indeed the case. What about 42*(1/2)t ?
  3. Is this the only function that satisfies this relation? What about cos(2*pi*t)*(1/2)n? Can you find other functions that satisfie that now?
If we want (1/2)t to be the only solution, we need to add an extra condition. This is exactly what we did in the previous section when we used a symmetry argument to find the value of N(1/2). Using the diagrams above, we realized that N(1/2 + 1/2) should be equal to N(1/2) * N(1/2), and that N(1/3 + 1/3 + 1/3) should be N(1/3)3.
  1. Using the same symmetry argument show that N has to satisfy N(t+s) = N(t)*N(s)
  2. Suppose now that N is differentiable, use the limit definition of the derivative to show that N satisfies the following equation:
    where K is N'(0)
  3. What are the possible solutions now?

The last question makes it obvious now why the radioactive decay of Carbon is called exponential. The number of atoms that decay at a given time is directly proportional to the number of atoms present in the sample.

Compound Interest

Another very close example and good application can be found in the theory of compound interest, where the exponiential decay becomes an exponential growth.

The idea here is to model a process where the amount of money available grows by -- say -- 5 % every year. There are many ways of modeling such a process, depending on the properties wanted for the model. To read more about this, check this article