In this Activity we will investigate how your calculator's [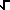
] (squared-root) key works. You might
wonder how you would compute a square-root yourself, or at least how
you would approximate it. If you answered "I would use my calculator",
remember that someone had to program your calculator to
approximate the square root of a number, so that doesn't really answer
the question of how one might carry out such an approximation.
Notice what happens when you repeatedly press the [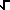] key on your calculator. Let's try this
with 5 as the initial input number and see what sequence of numbers we
get:
- 5
- 2.23606...
- 1.49534...
- 1.22284...
- 1.10582...
- 1.05158...
- 1.02546...
- . . . . . .
It looks like the fractional part is roughly
halved at each successive stage, that is, each time we take the
square-root, the next number we get seems to have a fractional part
about half that of the preceding number. But it can't be
that that is all our calculator really does!
What is going on?
Let's investigate...
- Does this process take place if we start with a number other
than 5? Do you think this happens for all? most? some? choices for
initial value? Experiment.
- When does this "halving" phenomenon happen in general? How big
or small does the input number have to be?
- Did you investigate also what happens when your input number
is a fraction?
Follow the steps below, assuming you are dealing with input
numbers of the sort which you have experimentally determined would
produce the "roughly half the fractional part" phenomenon.
Part A: Non-calculus Method
- (1)Let s be a "small", positive number.
Then our observation that "the fractional part is roughly halved at
each stage" can be mathematically described by:
- The square-root of 1+s is approximated by (
1+s)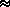 
__________
- (2) Give an informal proof/justification for this "approximate
equality" by analyzing what you get by squaring both sides.
- (3) If x=1+s then another way to describe our
observations mathematically is:
- The square-root of x is approximated by (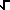x)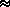
_____________
(You should fill in the blank with an expression in terms of x)
- (4) Give an informal proof/justification of (3)
Part B: Calculus to the Rescue!
- (1) Use the Taylor series of f(x)= (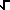x) at c=1 to give a more formal
justification of your approximation in part (A)(3). You may
assume that f(x)is equal to it's Taylor series,
T(x),so that you need only show that T(x)is
approximated by the right-hand side of the approximation
(A)(3).
- (2) Now use Taylor's Theorem with Remainder to quantify
how good an approximation the approximate-equality in (A)(1)
is. For example, if x is within 1/100 of 1, how good an approximation
of the square-root of x is the right-hand side of (A)(3)?
Copyleft
notice: Copyright ©
1995, by Harel
Barzilai -- "Share and Enjoy".
Non-profit educational use explicitly allowed and
encouraged.
May not use for any other purpose without written
permission.
Return to Projects Calculus Home
Page
