Series, Integrals, and Hidden Patterns

Series, Integrals, and Hidden Patterns

(1)The figure below indicates a pattern for the creation of infinitely many boxes inside a triangle in the plane. Suppose the base of the triangle is of length two.

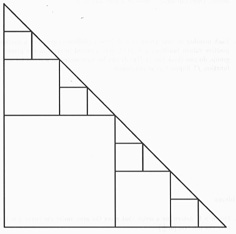
(a) What is the area of the largest box?

(b) What is the total area of the two next largest boxes?

(d) If you drew in more boxes, how many would there be at the next stage? What would their total area be?

(e) What is the total area of the largest box plus the two next largest boxes? What is the total area of the 1+2+4=7 largest boxes together? If we added together the areas of all of the infinitely many boxes insides the triangle, what would the area be, assuming it makes sense to add up infinitely many areas? Should this answer match the total area of the triangle? Does it?

(2)(a) You probably computed the total area of the triangle in part (1) by using geometry. Compute the area now with an integral, by choosing a suitable f(x) and finding the area under (a portion of) its graph.

(b) We know that this integral, like all definite integrals, is in fact the limit of Riemann sums. Can you interpret the pattern of boxes inside the triangle in terms of Riemann sums?