
After several researchers die from 'accidents,' the team uses organizational theory to find other researchers working with the deceased. A conspiracy to defraud elections is uncovered, and Charlie publishes a paper to make the method of defraud common knowledge.
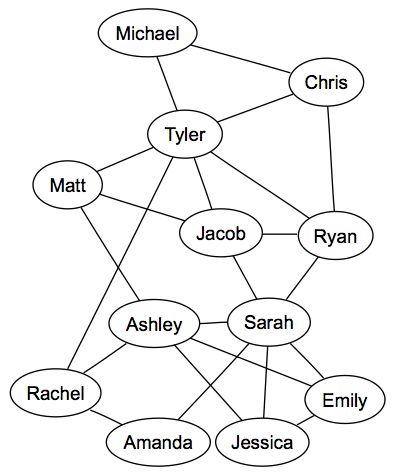
By analyzing how people are connected to each other in certain social contexts mathematicians have been able to study things as diverse as the spread of diseases and games like six degrees of Kevin Bacon. A social network is simply a collection of people and certain relationships between those people. To represent the network a graph is used. A graph consists of a set of vertices and edges (not necessarily straight lines) connecting vertices. Social networks represent people as vertices, relationships between people as edges. Below is a small example of a made up social network where two individuals are connected by an edge if they are friends. Real social networks are much more complicated; beside is a social network from a real high school where two individuals are connected if they are dating or have dated each other. You can read more about the dating network and see other networks here.


Social networks are common facets of our lives, and it is likely that you belong to some specific network that some scientist has studied. Many social networking sites like Facebook and Myspace have been the subject of scientific studies. Also, vertices are not just limited to people; the internet can be viewed as a network with edges representing links. Some scientists have even studied the interaction of proteins in your body as a network.
Many different network properties can be studied mathematically. A basic property is the distance between two vertices. If each edge has length 1, the distance between two vertices is the length of the shortest path connecting those vertices. Another property is the diameter of the network, which is the longest shortest path in the network. Another basic property is the degree of a vertex, i.e. the number of edges that touch a vertex. The distribution of the degrees of a network is another important property. Many networks such as social networks, protein interaction networks and the internet have been found to have power law distributions, that is the probability that a vertex is connected to n other nodes is proportional to n-a for positive a. Other properties of graphs can be found using advanced techniques. There are algorithms to find the most influential vertices in a network, and algorithms that can find closely related vertices in a network. In fact some algorithms can identify web pages which are about related topics without knowing the contents of the webpages just by analyzing links.