Dimension
In this section we will discuss dimension and find ways to think about
4 dimensional space.
Let's start with 1 dimension. A 1 dimensional space is going to be a
line that extends in either direction an infinite amount.

Between any two locations on the line we want to only have the
property of length and to _not_ have the properties of width or
height, so we will imagine the line to be infinitesimally thick, which
means essentially that it has no thickness.
We can think of the line as made up of an infinite number of
locations, or points. These are places on the line and they have
neither length nor height nor width.
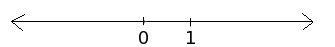
We can label some point 0 and some other point 1 and this makes our
line into a number line, since now we have a scale to measure
distance.
Let's play a guessing game now. I'm thinking of a number and you guess
what it is. Hint: I'm thinking of -2.8. Okay, that's not much of a
game, but the point is it takes me exactly one number to specify a
point on this line. For every point there is a number and for every
number there is a point.
Definition. Given a space the number of numbers needed to specify a
particular point is called the dimension of the space.
In the example above, the line is 1 dimensional, since it takes 1
number to specify a given point.
We can imagine what it would be like if our universe had only 1
dimension. Beings would have to be worm like and no two could ever
pass each other

without passing through each other. It's not a happy prospect, as
there is little a one dimensional critter can do to entertain itself.
Think of some activity you enjoy that a one dimensional creature could
never enjoy.