| Back to Section Page | Back to Problems Page |
Practice Problems for 3/18
- A certain type of slug has a semicircle cross section, where the rounded part of the semicircle is its back. The slug is always 5 times as long as it is high. When the slug is 10 inches long, it grows (lengthwise) at a rate of .2 inches per week.
- At what rate is the slugs volume increasing when it is 10 inches long?
- How fast is the area of the slug's belly (the part of the slug that touches the ground) growing when it is 10 inches long?
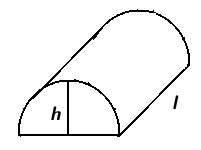
a) We want to find \(\frac{dV}{dt}\) when \(l=10\).
The volume of the slug is half the volume of a cylinder with radius \(h\) and height \(l\). Since \(h=l/5\) we have \(V=V(l)=\pi h^2l=\pi \frac{l^2}{25}l=\frac{\pi}{25}l^3\). Taking the derivative of both sides with respect to \(t\) gives \[ \frac{dV}{dt}=\frac{3\pi}{25}l^2\frac{dl}{dt}. \] So, when the slug is 10 inches long, the rate of change of the volume is \[ \frac{dV}{dt}|_{l=10}=\frac{3\pi}{25}{100}(.2)=\frac{12\pi}{5} in^3/week. \]
b) We want to find \(\frac{dA}{dt}\) when \(l=10\).
The area of the slugs belly is the area of a rectangle with width \(h\) and height \(l\). Since \(h=l/5\) we have \(A=\frac{1}{5}l^2\). Taking the derivative of both sides with respect to \(t\) gives \[ \frac{dA}{dt}=\frac{2}{5}l\frac{dl}{dt}. \] Thus, when the slug is 10 inches long, the rate of change of the area of its belly is \[ \frac{dA}{dt}|_{l=10}=\frac{2}{5}(10)(.2)=\frac{4}{5} in^2/week. \]