| Back to Section Page | Back to Problems Page |
Practice Problems for 3/20
- Use an appropriate linearization to approximate the value of \(f(x)\) for \(x=1.1,1.23\) and 1.38 using the information in the table below.
x f(x) f'(x) 1 0.7854 .5 1.2 0.8761 .4098 1.4 0.9505 .3378 - To approximate \(f(1.1)\), we use a linear approximation centered at \(a=1\). In this case
\[
L(x)=f(a)+f'(a)(x-a)=0.7854+.5(x-1),
\]
and thus the approximation would be \(f(1.1)\approx L(1.1)=0.7854+.5(.1)=0.8354.\).
It would be equally valid to use \(a=1.2\) as the center since it is the same distance from 1.1. In this case, the linearization would be \[ L(x)=0.8761+.4098(x-1.2), \] and thus the approximation would be \(f(1.1)\approx L(1.1)=0.8761+.4098(1.1-1.2)=0.8761+.4098(-.1)=.83512.\) We can't say which approximation is better, however, they agree up to the thousands place, so either one is probably fine. - To approximate \(f(1.23)\), we use a linear approximation centered at \(a=1.2\) since it is the closest point for which we have information. \[ L(x)=0.8761+.4098(x-1.2), \] and thus the approximation would be \(f(1.23)\approx L(1.1)=0.8761+.4098(1.23-1.2)=0.8761+.4098(.03)=.888394.\)
- To approximate \(f(1.38)\), we use a linear approximation centered at \(a=1.4\) since it is the closest point for which we have information. \[ L(x)=.9505+.3378(x-1.4) \] and thus the approximation would be \(f(1.38)\approx L(1.38)=.9505+.3378(-.02)=.943744.\)
- A tracking telescope located 3000 meteres from the launch platform is begin used to track a small rocket. Two seconds after the launch, the angle of inclination of the rocket is measured to be 1.117 radians, with a possible error of \(\pm .0349\) radians (which is \(2^{\circ}\), fyi). How high is the rocket and what is the possible error in this calculated height? (Use radians in your calculations and round at least to three decimals to the right of the decimal point.)
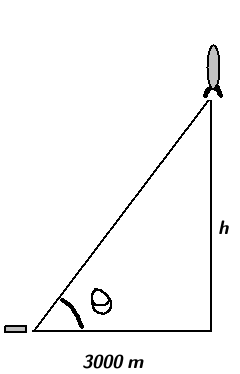
First, find a function of the height of the rocket in terms of the angle of inclination, which we will denote as \(\theta\). From the diagram we see \[ h=h(\theta)=3000\tan(\theta). \] We also know that \(\theta \in (1.0821,1.1519)\). This indicates we should approximate \(h\) using a linearization centered at \(.0349\) radians. (We pick \(a=1.117\) because this is the center of the interval containing the possible values of \(\theta\).) This gives \[ h(\theta) \approx L(\theta)=h(1.117)+h'(1.117)(\theta-1.117)=6150.744+15610.551(\theta-1.117) \] where we have rounded off to the thousands place.
This tells us that the change in \(h\) is approximated by \[ \Delta h \approx 15610.551\Delta \theta. \] So since \(|\Delta \theta| \leq .0349\), we know \(\Delta h \approx 544.808\) m. Thus, the height is \(h(1.117)\pm \Delta h \approx 6150.744 \pm 544.808 \) m.