| Back to Section Page | Back to Problems Page |
Practice Problems for 4/8
-
Let \(f(x)\) be a twice differentiable function. If \(x=c\) is a critical point of the function \(f'(x)\), which of the follow is true and WHY?
- \(c\) is always an inflection point of \(f(x)\).
- \(c\) is only an inflection point of \(f(x)\) if \(f'(c)\) is a local maximum or local minimum value of \(f'(x)\).
- \(c\) is only an inflection point of \(f(x)\) if \(f(c)\) is a local maximum or local minimum value of \(f(x)\).
The correct answer is b. - Find all inflection points of \(f(x)\) and determine on which intervals \(f(x)\) is concave up, and on which intervals it is concave down.
- \(f(x)=x^4-4x^3+10\)
- \(f(x)=\frac{1}{12}x^4-\frac{1}{3}x^3+\frac{1}{2}x^2+x\)
Inflection points are where the concavity of a curve changes. Possible points of inflection are the critical points of \(f'(x)\). - \(f''(x)=12x^2+12x-24=12(x^2+x-2)=12(x+2)(x-1)\). So, there may be an inflection point at \(x=-2\) and at \(x=0\). To determine whether or not each point is truly an inflection point, we must verify that the sign of \(f''(x)\) changes.
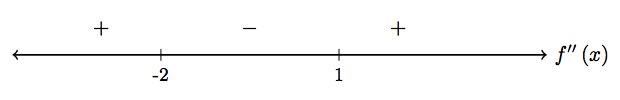
- \(f''(x)=x^2-2x+1=(x-1)^2\). So, the only possible inflection point is \(x=1\).

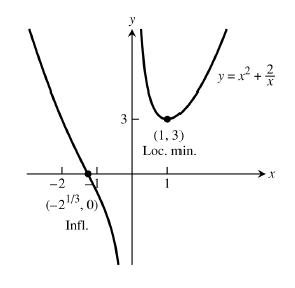
- Graph the function \(f(x)=x^2+\frac{2}{x}\).
\(c\) is an inflection point if \(f(x)\) changes concavity at the point \(c\). Since the concavity is determined by whether \(f''(x)\) is positive or negative, a change in concavity means \(f''(x)\) changes from positive to negative or negative to positive as it passes through \(c\).
Since \(f''(x)\) is the first derivative of the differentiable function \(f'(x)\), this would mean that the critical point must be a local maximum or minimum value of \(f'(x)\). If the critical point \(c\) is not actually a local maximum or minimum of \(f'(x)\) we know it must be that the derivative of \(f'(x)\) doesn't change sign as \(x\) passes through \(c\). This would mean that \(f''(x)\) doesn't change sign, and thus concavity does not change.
\(f'(x)=2x-\frac{2}{x^2}\) for \(x\neq 0\). Techincially \(x=0\) is a critical point, but since \(x=0\) is a vertical asympotote, there cannot be a local extreme value here. There is one critical point of type I, which is \(x=1\).
\(f''(x)=2+\frac{4}{x^3}\) for \(x\neq 0\). \(f''(1)>0\), so, by the second derivative test, there is a local minimum \(x=1\). Note that \(f(1)=3\).
Inflection points: \(f''(x)=0\) if \(x^3=-2\). That is, if \(x=\sqrt[3]{-2}\). This is an inflection point since \(f''(x)>0\) for \(x<\sqrt[3]{-2}\), and \(f''(x)<0\) for \(x>\sqrt[3]{-2}\). Thus, the concavity changes from up to down at \(x=\sqrt[3]{-2}\), and \(f(\sqrt[3]{-2})=0\). Putting this all together gives the graph: