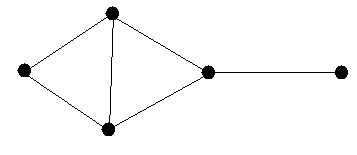
A graph is a collection of vertices, and some edges that connect pairs of vertices. For example, the following graph has five vertices and six edges. Dots are vertices and lines connecting two dots are edges.

For more complicated graphs, we may make edges cross each other or even curve around vertices. This has no significance; all that matters is which pairs of vertices are connected by an edge and which are not.

The paper is mainly interested in cliques of graphs. A clique is a set of vertices such that every pair of them forms an edge. A set with 0 or 1 vertices is automatically a clique. A set of 2 vertices is a clique precisely if they are connected by an edge. The set of three vertices on the far left above form a clique, for example. The set of three furthest to the top right do not form a clique, however, as the top vertex and the far right one are not connected by an edge.

If we have a graph, we can count its cliques of various sizes. Every graph has 1 clique on zero vertices, as there is exactly one way to pick none of the vertices. There are 5 cliques on one vertex (the five vertices) and 6 cliques on two vertices (the six edges). There are also two cliques on three vertices (the vertex sets of the two triangles). We can list these numbers to get the face vector of the graph. In this example, we get (1, 5, 6, 2).

The main problem to address is what integer vectors can possibly be face vectors of graphs. For example, if we have 5 vertices, the above graph shows that we could have six edges. By making all possible pairs of vertices connected by an edge, we could have 10 edges. But a graph with five vertices cannot possibly have more than ten edges.

The problem becomes harder if we are dealing with larger cliques. For example, if a graph has 60 cliques on three vertices, then what is the most cliques on four vertices it could possibly have? Unlike where we start with vertices, there isn't an obvious way to maximize this.

This paper is mainly interested in answering the question of, if a graph has some particular number of cliques on k vertices, what is the greatest number of cliques on k+1 vertices it could have? The Kruskal-Katona theorem gives some upper bounds for a more general construction called simplicial complexes. These bounds apply to our situation with graphs, as well. They are not sharp for graphs, however.

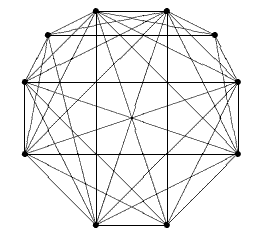
For example, the Kruskal-Katona theorem says that a graph with 9 cliques on 3 vertices can have at most 3 cliques on 4 vertices. What the theorem does not say is that such a graph cannot have 3 cliques on 4 vertices, either; the best possible is only 2 cliques on 4 vertices. We give better upper bounds.

The basic idea is that a previous paper gives some upper bounds that also depend on the size of the largest clique in the graph. If the largest clique is "small" (that is, not as large as it could have been), these bounds are better than those of the Kruskal-Katona theorem. If the largest clique is "large" (that is, as large as it can possibly be), the bounds of the previous paper usually coincide with those of the Kruskal-Katona theorem. In this case, we prove some new bounds that are usually better.

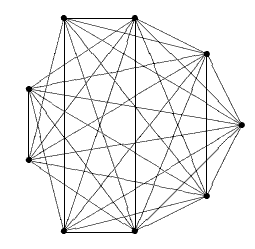
We also show that even if we could get perfect upper bounds on consecutive face numbers, it would not be enough to characterize the face vectors. For example, a flag complex with 70 2-dimensional faces can have at most 85 3-dimensional faces. This bound is sharp, as shown by the following graph.


A flag complex with 85 3-dimensional faces can have at most 62 4-dimensional faces. This bound is also sharp, as shown by the following graph.

But a flag complex with 70 2-dimensional faces can have at most 61 4-dimensional faces, whether it has 85 3-dimensional faces or some other number of them.