

A hyperplane is subset of a space that is of dimension one less. For example, lines are hyperplanes of a 2-dimensional plane, and planes are hyperplanes of a 3-dimensional space. The analogous concept carries over to higher dimensions, and a hyperplane divides a space in half, such that every point not in the hyperplane is on one side of it or the other.
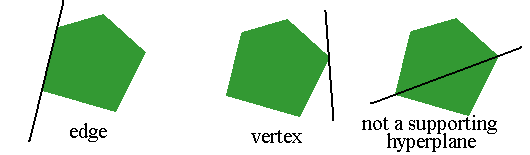
A face of a polytope is an intersection of the polytope with a hyperplane such that the entire polytope lies on the same side of the hyperplane. Such a hyperplane is called a supporting hyperplane. For example, the faces of a polygon are the vertices and edges. The faces of a cube are the vertices, edges, and squares.
A simplicial polytope (technically, the boundary of a simplicial polytope) is a flag complex if every minimal set of vertices that is not the vertex set a face is a two element set. In other words, suppose that we pick a set of vertices, and suppose that our set of vertices is not precisely the set of vertices contained in any particular face. Then if the polytope is a flag complex, then some two of the vertices in our set must not be contained in a common edge.
For example, a tetrahedron is not a flag complex. If we pick all four of the vertices, they do not form a face, as a face would have to be contained in a 2-dimensional plane. Every pair of vertices does form an edge, however. On the other hand, an octohedron is a flag complex.
Each face is of some particular dimension. For example, vertices are 0-dimensional faces, edges are 1-dimensional, and so forth. We can count the number of faces of any particular dimension to get the face numbers of a simplicial polytope. The number of faces of dimension i is denoted fi.
Charney and Davis conjectured a linear inequality on the face numbers simplicial polytopes that are flag complexes. More precisely, if the polytope is of even dimension 2d (so that its highest dimensional faces are of odd dimension 2d-1), they conjectured that (-1)d(1 - (.5)1f0 + (.5)2f1 - (.5)3f2 + ... + (.5)2df2d-1) is nonnegative.
It is possible to use some equations known as the Dehn-Sommerville relations to rearrange this somewhat. Once this is done, if d=1, the Charney-Davis conjecture basically asserts that any polygon that is not a triangle (since a triangle is not a flag complex) has at least four vertices. If d=2, the conjecture asserts that f1 - 5f0 + 16 is nonnegative. The conjecture has also been proven in this case by Davis and Okun, but the proof is horrendously long and messy. In higher dimensions, the conjecture remains open.
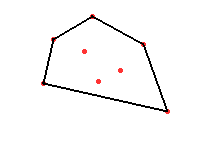
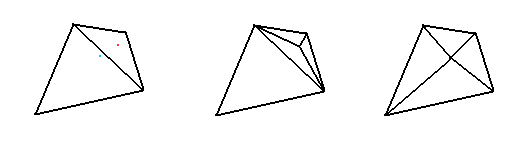
The main other case known regards subdivisions. Recall that a polytope is a convex hull of finitely many points. We can take a stellar subdivision of a face of a polytope by adding another point very slightly above one face to break up that face. The next picture shows how if we start with a tetrahedron and add either the red or blue point, we can subdivide either a triangle or an edge.
We show that it is enough to subdivide only the odd-dimensional faces, in addition to as many or as few of the even dimensional faces as one prefers. We thus show that the Charney-Davis conjecture is true for somewhat coarser subdivisions than previously known.