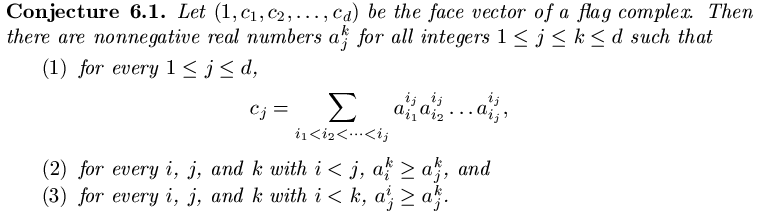
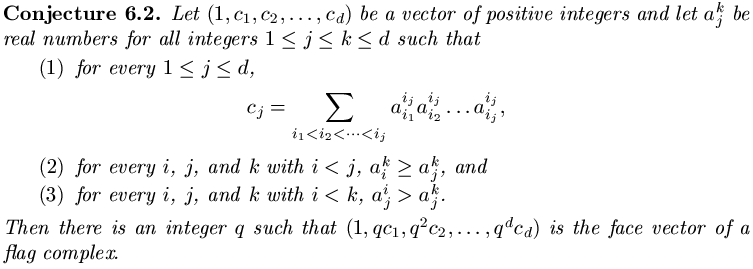
A simplicial complex is called a flag complex if all minimal non-faces are two element sets. Flag complexes are the same thing as clique complexes of graphs. Since flag complexes are simplicial complexes, the bounds of the Kruskal-Katona theorem apply to flag complexes. However, they are not sharp for flag complexes. For example, a simplicial complex with 9 two-dimensional faces can have up to 3 three-dimensional faces. A flag complex with 9 two-dimensional faces can have no more than 2 three-dimensional faces.

There are various bounds that say, in order for an integer vector to be the face vector of a flag complex, it must satisfy these bounds. This only gives us a way to say that a given integer vector does not correspond to any flag complex. What if we want to go the other way, and say that this integer vector does correspond to a flag complex, and here it is?

Obviously, this cannot be done with an arbitrary integer vector, as some simply don't correspond to any flag complex. Indeed, there isn't a known characterization of which integer vectors do correspond to flag complexes and which do not. What this paper does is to give a construction method that explains how to construct a flag complex corresponding to a large class of integer vectors.

There are two main barriers to characterizing the face vectors of flag complexes. One is that, unlike in the case of more general simplicial complexes, smaller dimensional faces can force there to be a lot of larger dimensional faces. As an extreme case, if a flag complex has 10 vertices and 45 edges, then it must have 120 triangles (faces of dimension two), as the complex must be a simplex on 10 vertices. A simplicial complex that is not flag could easily have 10 vertices, 45 edges, and no triangles at all, or any number of triangles between 0 and 120.

The other barrier is discreteness issues. When constructing a simplicial complex, we can easily add one face at a time and have a simplicial complex every step of the way. When constructing a flag complex, adding just one edge may add huge numbers of faces of larger dimensions. This can cause the face vectors of flag complexes to behave strangely.

For example, a flag complex with exactly 20 triangles can have as few as 15 edges. A simplex on six vertices gives an example of this. If we want the flag complex to have exactly 19 triangles, however, then it must have at least 17 edges. Having fewer triangles in this case requires more edges. If a flag complex has exactly 15 edges, then it could have exactly 17 triangles or exactly 20 triangles, but it cannot have exactly 18 or 19 triangles.

Still, this sort of messy holes can only happen in certain places. If one wants to associate integer vectors with lattice points in Euclidean space, then there are a pair of hypersurfaces such that on one side of both of them, none of the lattice points are face vectors on flag complexes. On the other side of both, all of the lattice points are face vectors of flag complexes. It is only in between them that we get the messy holes as in the previous paragraph--and there isn't really all that much space in between them. The hypersurfaces may be very messy globally, but they are reasonably well-behaved locally. Giving explicit bounds essentially specifies such a hypersurface.

The paper starts by giving a way to construct a flag complex with two particular specified face numbers, and giving bounds on the face numbers that ensure that the construction will work. These bounds are not far away from inequalities in the other direction that guarantee that there is no flag complex with the two specified face numbers. Indeed, the paper shows that asymptotically, the bounds guaranteeing that there is a flag complex with two particular face numbers are the best that we could realistically hope for.

There are also some cases that lie between the bounds on the two face numbers that would guarantee that the construction works and the bounds that would guarantee that there is no such flag complex. In this case, the construction often works, but not always. If the face numbers are near the bounds that would guarantee that it would work, then the construction nearly always does work. If the face numbers are near the bounds that would guarantee that there is no flag complex with the two specified face numbers, then the construction usually fails.

If you have a proposed face vector, however, that specifies the dimension of the flag complex. The paper next extends the previous construction to explain how to construct a flag complex of a specified dimension with two face numbers specified. As before, the paper gives bounds on when the construction is guaranteed to work, and these bounds aren't really that far away from bounds that would guarantee that the face vector does not correspond to any complex.

In this scenario, I can't prove that the bounds that guarantee that the construction works are asymptotically the best that we could realistically hope for, but the bounds are so similar to those of the unspecified dimension case that it seems likely that the bounds should still be very good. As with the case of unrestricted dimension, this construction nearly always works if near the bounds that would guarantee that it works, and usually fails if near the bounds that would guarantee that there is no flag complex corresponding to the given pair of face numbers.

But this only guarantees that we can construct a flag complex with two particular face numbers. If we want to construct a flag complex with a given face vector, we likely want the whole face vector. My construction for a complex with two face numbers and a given dimension readily generalizes to this situation. The construction says, start by constructing a flag complex with exactly the number of top dimensional faces that we want in a specified manner, and we are guaranteed that it uses relatively few faces of all smaller dimensions. Next, add in the remaining faces of the next highest dimension in a specified manner that avoids creating any larger dimensional faces, but again, adds relatively few smaller dimensional faces. Repeat this process for each dimension, adding in however many faces we still need to add of a given dimension at each step, without adding any faces of higher dimension and while adding relatively few faces of lower dimensions.

Finally, I have two conjectures that, taken together, would be tremendous progress toward characterizing the face vectors of flag complexes.

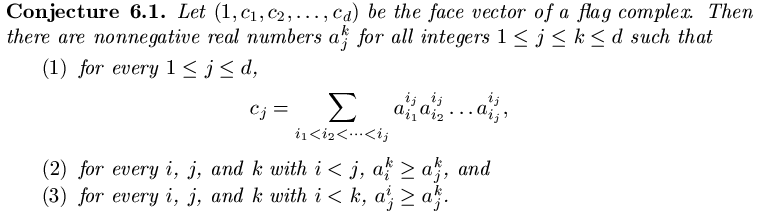
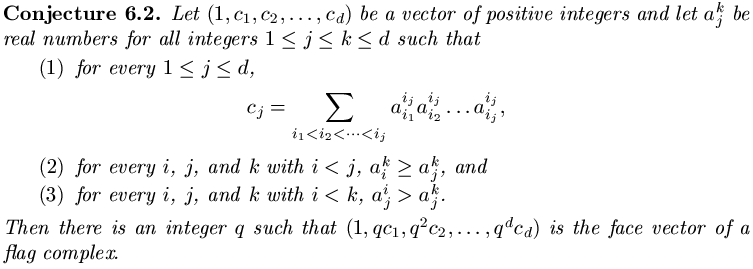
Furthermore, the second conjecture is true. One proof sketch that I find rather convincing is that if we assume all a_j^k are rational numbers, rather than merely real, then I have an easy proof that it is true, which basically consists of applying my main construction. There are so many more a's than c's that one can almost certainly tweak the a's slightly to make them rational while preserving the equalities of the first condition.

Additionally, I more or less know how to give a proper proof of the second conjecture that would additionally show that if the strict inequality in the third condition is always a large enough difference between the two constants, then we can take q = 1 and it will work. That would say that (1, c₁, c₂, ..., c_d) is, itself, the face vector of a flag complex, as my construction would work to give the explicit complex. The proof would probably be very long and messy, which is why I haven't done it, but intuitively, it has to work, as it would essentially be formalizing the proof sketch of the previous paragraph.