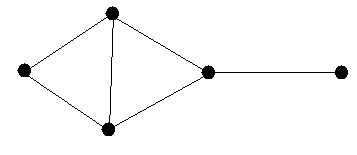
The paper is mainly interested in cliques of graphs. A clique is a set of vertices such that every pair of them forms an edge. A set with 0 or 1 vertices is automatically a clique. A set of 2 vertices is a clique precisely if they are connected by an edge. The set of three vertices on the far left above form a clique, for example. The set of three furthest to the top right do not form a clique, however, as the top vertex and the far right one are not connected by an edge.

If we have a graph, we can count its cliques of various sizes. Every graph has 1 clique on zero vertices, as there is exactly one way to pick none of the vertices. There are 5 cliques on one vertex (the five vertices) and 6 cliques on two vertices (the six edges). There are also two cliques on three vertices (the vertex sets of the two triangles). We can list these numbers to get the face vector of the graph. In this example, we get (1, 5, 6, 2).

Now suppose that instead of starting with a graph and computing the face vector, we start with a proposed face vector and try to find a graph that has that particular face vector. Sometimes, it cannot be done. For example, if we have five vertices, then we cannot have more than ten edges, as there are only ten ways to pick two of the vertices.

Given a face vector that does correspond to a graph, this paper explains a method to construct the graph that has exactly the given face vector. It doesn't always work, and indeed, it isn't known exactly which face vectors correspond to some graph and which do not.