Dynamical systems with multiple time scales are also called singularly perturbed systems and slow-fast systems. The theory of systems with multiple time scales has been approached from at least three complementary viewpoints: nonstandard analysis, "classical" asymptotic methods, and geometric methods that have come to be called geometric singular perturbation theory. The research has been shaped both by a few seminal examples and a desire to characterize typical or generic behavior in these systems. These efforts have been limited by difficulty in computing unstable trajectory segments, called canards, and by difficulty in comprehending the complex geometry of solutions. My research seeks to advance the frontiers through better algorithms and more theory. There are several examples that I have studied extensively, as well as theoretical developments that I have pursued.
Forced van der Pol Equation
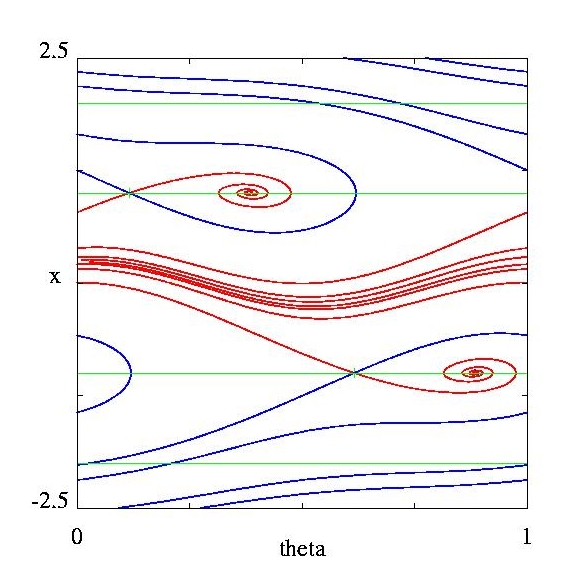
The forced van der Pol equation is the first "dissipative" system in which the phenomenon of chaos was observed. Dissipative systems are ones that are not symplectic; i.e., do not have the form of conservative mechanical systems. As an autonomous vector field, the forced van der Pol equation is a three dimensional system with two slow and one fast variable. One of the variables is a cyclic variable representing the periodic forcing term in the system. The system was studied extensively by Cartwright and Littlewood during the 1940's and 1950's, resulting in a lengthy proof for the existence of chaotic behavior in this system. The details of their work have been difficult to understand. I have worked with Kathleen Hoffman, Warren Weckesser, and my students to simplify and extend their results. Our approach has been based upon geometic singularity theory. In the singular limit, the system reduces to a slow flow on a two dimensional critical manifold but there are folds at which trajectories from the two sides of the fold meet one another. The limiting dynamical behavior of the system at these folds is to jump along the direction of the fast variable to a new point of the critical manifold. The slow flow and jumps are amalgamated into a hybrid dynamical system, and the bifurcations of this hybrid dynamical system are studied. The picture below depicts a phase portrait of this system. The two sides of the box are glued to each other, forming a cylinder. When a trajectory reaches the line x = 1, it jumps vertically to the line x = -2, and when a trajectory reaches the line x = -1 it jumps vertically to the line x = 2. The blue trajectories are stable manifolds of folded saddles that are special in that trajectories reaching these points have a wider range of options: they can jump, they can turn to follow the unstable manifolds of the folded saddles, or they can continue along the stable manifold into the region -1 < x < 1, forming special trajectories called canards. After following the stable manifold an arbitrary distance in this region, the canards can jump vertically, either up or down, to new points on the critical manifold.

From the slow flows like the one depicted above, we construct discontinuous one dimensional return maps for the line x = 2 that give the singular limit of two dimensional Poincare return maps for the system. We characterize bifurcations of the return maps and use these to identify parameter ranges in the system with distinct types of dynamical behavior. The thesis of Radu Haiduc extends our analysis with theoretical analysis and computer proofs that produce parameter values for which the three dimensional flow is structurally stable and possess a chaotic invariant set. This strengthens the results of Cartwright and Littlewood and completes research begun by Smale to give a geometric characterization of the dynamics of this system.
A Modified van der Pol System
The chaotic dynamics of the forced van der Pol system described above occur in invariant sets that are not attractors. Indeed, these invariant sets are highly unstable and elusive to approximate with numerical simulations. The trajectories comprising the invariant sets contain canard segments that lie along unstable sheet of the slow manifold. Numerical solutions which come close to the unstable sheet of the slow manifold fly away from it on the fast time scale of the system. Even round-off errors are amplified fast enough by the instability to prevent trajectories from remaining close to the unstable sheet for a substantial distance. There is a second reason why the chaotic invariant sets in the forced van der Pol system are difficult to display. The invariant sets discovered by Cartwright and Littlewood are not attractors. This means that trajectories with typical initial conditions do not tend to the invariant set. In the example described by Haiduc, almost all trajectories tend to periodic orbits.
The presence of chaotic attractors in discrete dynamical systems has been studied intensively in the context of iterations of one dimensional maps and a two dimensional diffeomorphism called the Henon map. Numerical simulations of these examples suggested that there are large sets of parameters for which the maps do have chaotic attractors. An extensive body of research has now verified this observation. Qiudong Wang and Lai-Sang Young formulated a list of hypotheses that are sufficient to prove that families of two-dimensional maps satisfying these properties have positive measure sets of parameters for which the maps have chaotic attractors. Thus, there is a positive probability that a map with randomly chosen parameters in one of these families will have a chaotic attractor. The families of maps studied by Wang and Young are almost singular: the maps become non-invertible one dimensional maps when a small parameter becomes zero.

Two Coupled Neurons
Kathleen Hoffman, Warren Weckesser and I investigated a singularly pertubed system with two slow and two fast variables that is a caricature of a pair of neurons coupled by reciprocal inhibition. We used the computer program AUTO to investigate periodic solutions in this system. The results of this investigation are intriguing and perplexing. With one parameter allowed to vary, AUTO computes a continuous family of periodic orbits. This family encounters numerous canards and bifurcations. Thus far we have examined a few of the orbits in detail, characterizing the different types of canards they encounter. The image below shows a three dimensional projection of one of these trajectories onto a coordinate subspace with the two fast and one slow variable.
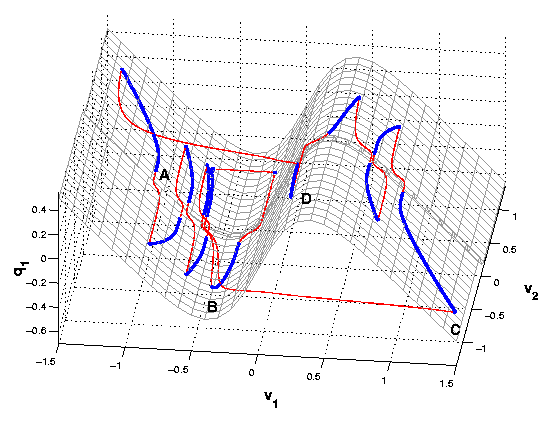
There are three canards in this trajectory, created by two different mechanisms. The paper Numerical Computation of Canards contains a description of the model and technical details of this work.
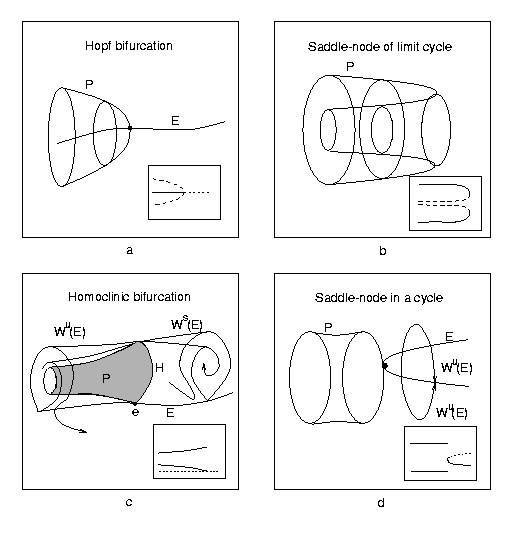
Death of Periodicity
Bifurcation theory can be used to interpret the complex rhythmic properties of neurons. Rinzel pioneered the interpretation of bursting oscillations of membrane potential in terms of dynamical systems with multiple time scales. My work with Allan Willms, Ronald Harris-Warrick and Jack Peck (Bifurcation,bursting and spike frequency adaptation, J. Computational Neuroscience, 4, 257-277, 1997) quantifies such analysis and apply it to the analysis of spike trains from a neuron in the stomatogastric ganglion. Spike frequency adaptation describes the phenomenon that occurs when the frequency of a neuron firing action potentials slows from its inception. This widely observed phenomenon can lead to the "death of periodicity" with the frequency slowing to the point at which the firing ceases. Viewing the oscillations as those of a dynamical system with a slowly varying parameter, we associate the death of periodicity with bifurcations that occur in the "frozen" system in which the evolution of the slow parameter is halted. Different types of bifurcations yield different asymptotic rates at which frequency of the oscillation tends to zero. We demonstrate that these predictions are valid in model systems and discuss a new type of bifurcation that leads to the death of periodicity. Finally the analysis is applied to spike train data from the LP neuron of the STG. The image below sketches four different types of bifurcations that lead to the death of periodicity. Families of periodic orbits to the left of each panel terminate in a bifurcation as a parameter varies along the horizontal axis.