The ground process is a simple model of evolution.
It has predictive strength and permits a clean description
of the new algorithm. The ground process is really a complex
parameter and a different process may be
substituted without essential changes to our algorithm.
For example, we could use the process of [TKF2],
which allows different substitution
models for transitions and transversions.
The ground process evolution model is that beginning with
an ancestor sequence ![]() , the sequence of each generation
is mostly copied faithfully to the next generation,
and occassionally letters are
substituted, deleted, or inserted.
The frequency of these events is
expressed per letter, per evolutionary distance, i.e. time.
, the sequence of each generation
is mostly copied faithfully to the next generation,
and occassionally letters are
substituted, deleted, or inserted.
The frequency of these events is
expressed per letter, per evolutionary distance, i.e. time.
The ground process is reversible. The probability
for a particular letter at a certain point to be deleted is
the same as the probability to insert that particular letter at a that
point. Substitution of letter ![]() for letter
for letter ![]() has the same
probability as the reverse substitution.
has the same
probability as the reverse substitution.
For sequences ![]() and
and ![]() , let
, let
A consequence of reversibility is
We describe the ground process in two parts: the development of an evolutionary history, and the specification of the letters which fill that history.
The start state of the machine writes column zero
| |
An evolutionary history is a sequence of transitions beginning at
start and ending at termination. Define the fate of a nonblank
symbol in the ![]() sequence (top or first member of pair)
as the sequence of columns beginning
with that symbol and ending just before the column with the
next nonblank symbol in the
sequence (top or first member of pair)
as the sequence of columns beginning
with that symbol and ending just before the column with the
next nonblank symbol in the ![]() sequence. The fate of
sequence. The fate of ![]() is start followed by some number of insertions. The fate of
is start followed by some number of insertions. The fate of
![]() is either homology or deletion followed by some number of
insertions. The fate of
is either homology or deletion followed by some number of
insertions. The fate of ![]() is termination.
is termination.
The parameters for determining the probability of an evolutionary
history according to a ground process are the insertion rate ![]() expressed per base per time, the deletion rate
expressed per base per time, the deletion rate ![]() , and the
evolutionary distance
, and the
evolutionary distance ![]() . We compute the probabilities using
the limit for large
. We compute the probabilities using
the limit for large ![]() of a discrete process with insertion rate
of a discrete process with insertion rate ![]() per base,
deletion rate
per base,
deletion rate ![]() per base. The resulting probabilities
are expressions in
per base. The resulting probabilities
are expressions in ![]() and
and ![]() .
.
Let
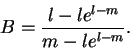
The probability for ![]() to be part of an evolutionary
history with
to be part of an evolutionary
history with ![]() insertions is
insertions is
The probability to extend ![]() by another letter is
by another letter is ![]() .
The probability to transition to end is
.
The probability to transition to end is ![]() .
.
Given that ![]() is extended by another letter, we have the
following probabilities.
The probability for homology followed by zero insertions
is
is extended by another letter, we have the
following probabilities.
The probability for homology followed by zero insertions
is
The probability for deletion followed by zero insertions
is
For the start and homology events, every successive
insertion is with probability ![]() , but for a deletion event,
the probability of the first insertion is different.
The ground process in [TKF] is presented
as a machine with a deletion state that has different transition
probabilities from the other states for this possible first insertion.
, but for a deletion event,
the probability of the first insertion is different.
The ground process in [TKF] is presented
as a machine with a deletion state that has different transition
probabilities from the other states for this possible first insertion.
The insight of [HWKMW], extended in [LMSH], is the description of the ground process using one main state and multiple transitions, including a ``forbidden transition'' with negative transition factor to accomplish the same result. The forbidden transition is from a deletion event with zero insertions to an insertion event.
The evolutionary history is completed to a sequence alignment
by writing a letter from the alphabet ![]() in place of each
in place of each
![]() .
.
The ground process has parameters
![]() which
define a distribution of letters. The parameter
which
define a distribution of letters. The parameter ![]() determines
the subsitution rate per base per time. As above, the equations
can be expressed in terms of
determines
the subsitution rate per base per time. As above, the equations
can be expressed in terms of ![]() .
.
The probability for an insertion
or deletion process to produce a letter ![]() is
is ![]() .
For a homology event, the probability for the ground process to produce
the pair
.
For a homology event, the probability for the ground process to produce
the pair ![]() is
is ![]() , where
, where
The computation of the array ![]() for sequences
for sequences
![]() and
and ![]() is recursive.
The base cases are
is recursive.
The base cases are ![]() with either index negative is zero
and
with either index negative is zero
and
![\begin{eqnarray*}
P(i,j) & = & P(i-1, j) \cdot B \pi_{{\bf A}[i]} +
P(i, j - 1)...
... \\
& & P(i-1, j-1) \cdot B^2 \pi_{{\bf A}[i]}\pi_{{\bf B}[j]}.
\end{eqnarray*}](img87.png)
The probability to observe ![]() and
and ![]() related by some evolutionary history is
related by some evolutionary history is
![]()