New constructions for visualization

Computing evolutionary history using the sequences ${\bf A}$ reversed and ${\bf B}$ reversed is computationally the same problem as for ${\bf A}$ and ${\bf B}$ as given.

Let $P^\vee(i,j)$ be the probability for the sequences ${\bf A}[i+1..l_{\bf A}]$ and ${\bf B}[j+1, l_{\bf B}]$ to align by some evolutionary history. Let $Q^\vee(i,j)$ be $P^\vee(i,j)$ normalized by the probability to observe the given sequences.

The base cases are

$$\begin{eqnarray*} P^\vee(l_{\bf A}, l_{\bf B}) & = & 1, \\ Q^\vee(l_{\bf A}, l_{\bf B}) & = & 1. \end{eqnarray*}$$

The equations for $P^\vee(i,j)$ and $Q^\vee(i,j)$ are the same as those for $P$ and $Q$, except progress is towards $i=0, j =0$ rather than away.

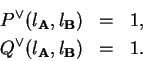
The product $P(i,j)P^\vee(i,j)$ is the probability ${\bf A}$ and ${\bf B}$ arose from some evolutionary history which restricts to an evolutionary history for ${\bf A}[1, i]$ and ${\bf B}[1, j]$, and for ${\bf A}[i+1, l_{\bf A}]$ and ${\bf B}[j+1, l_{\bf B}]$

Let

$$R(i,j) = Q(i,j)Q^\vee(i,j).$$

The entry $R(i,j)$ is the probability for an evolutionary history as for $P(i,j)P^\vee(i,j)$, providing for the artifactual truncation of sequence, divided by the probability that the sequences ${\bf A}$ and ${\bf B}$ were observed and the evolutionary history is start, $l_{\bf A}$ deletions followed by $l_{\bf B}$ insertions, end.

Every entry in $R(i,j)$ is comparable to every other entry. The contours near the maximum value of $R(i,j)$ bound the region containing the paths of the most likely alignments.

We propose another pair of arrays $S(i,j)$ and $S^\vee(i,j)$ which weight recent history more than distant history. We adapt the standard technique of approximating a sliding window by multiplying an accumulator by a factor between zero and one, and adding the new data value. An alternative interpretation is that we view the developing evolutionary history through a fog which makes distant states uncertain. The thickness of the historical fog is a parameter $\rho.$ The generic computation for $S$ is

$$\begin{eqnarray*} S(i,j) & = & \rho + (1-\rho)S(i-1, j) \cdot E + \\ & & (1-\rh... ...) / \pi_{B[j]}) -\\ & & (1-\rho)^2 S( i-1, j-1) \cdot E ^2, \\ \end{eqnarray*}$$

with suitable modifications at the boundaries.

Another model with the same mathematical description is that with probability $\rho \Pi_{{\bf A}[1, i]} \Pi_{{\bf B}[1,j]}$ the subsequences ${\bf A}[1, i]$ and ${\bf B}[1, j]$ are observed and discarded from consideration in the evolutionary history. The Smith-Waterman algorithm is a Viterbi path application of the similar idea that the alignment process might have optimal score applied to subsequences of ${\bf A}$ and ${\bf B}$.

We use the parameter

$$r = \rho^{-1} -1.$$

From the view of $\rho$ as the probability of a jump event, we call $r$ the odds against a jump event.

When $r = \infty$, and the other parameters are equal,

$$Q(i,j) = S(i,j).$$

We implement the computations

$$\begin{eqnarray*} J(i,j) & = & - \log S(i,j), \\ J^\vee(i,j) & =& -\log S^\vee(i,j), \\ W(i,j) & = & J(i,j) + J^\vee(i,j). \end{eqnarray*}$$

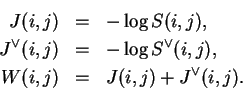
We also compute the equilibriuim value $\nu$ for noise given parameters $l, m, r, s$ and distribution $\pi$. This is the limit for large $i, j$ of $J(i,j)$ for long random sequences constructed from distribution $\pi.$

Using $\nu$, we can approximate $W(i,j)$ in any shape region by clamping the boundary values of $J(i,j)$ and $J^\vee(i,j)$ equal to $\nu$ when they are not otherwise actually calculated. This makes sense, for example, when we want to avoid computing on an area where we believe there is no alignment and want results for an adjacent area. We can also mask out a high scoring evolutionary history by forcing $J(i,j) = \nu$ on its path. This allows a second place ridge to be seen as maximum.