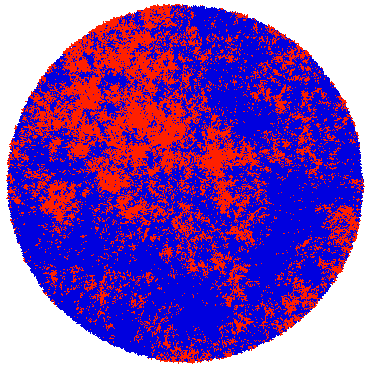
Laplacian growth is the study of interfaces that move in proportion to harmonic measure. Physically, it arises in fluid flow and electrical problems involving a moving boundary. This course will focus on Laplacian growth "from the inside", including sandpile models, internal DLA, rotor router, and the scaling limits of these models. The aim will be to see some basic tools of the trade -- harmonic functions, martingales, obstacle problems, quadrature domains, Green functions, smoothing operators -- in action as applied in recent research.

Possible additional topics if time permits: logarithmic fluctuations, abelian networks, and the proof by Pegden and Smart in 2011 of convergence of the abelian sandpile.

Prerequisites: Math 6110 or 6710. Some familiarity with martingales will be helpful. This course covers recent results in an active research area, but will be taught at a level accessible to beginning graduate students.

Book: Laplacian Growth, by Lionel Levine and Yuval Peres.
The book is still being written. A draft will be made available to students enrolled in the course.

Supplementary books (not required, but may occasionally come in handy):

• Harmonic Function Theory, by Sheldon Axler, Paul Bourdon, and Wade Ramey. Full text available online.
• Intersections of Random Walks, by Gregory F. Lawler

Links:

• Tobias Friedrich's rotor-router page (explore with Google Maps!)
• Sandpile app by Bryan Head and David Perkinson