 Knifty Knots (May 20, 2004)
Knifty Knots (May 20, 2004)
Introduction
To a mathematician, a knot is a loop in space. It can twist and turn, but eventually the beginning must meet up with the end. You can view some nice pictures of knots at the homepage of the knot theorist Morwen Thistlethwaite, http://www.math.utk.edu/~morwen/ . Knots have been an active area of mathematical research for over a century, and there are still unanswered questions.
Knot Diagrams
One way that knots are represented is by drawing a picture of the shadow of the knot and leaving gaps to indicate which part of the knot is lying below the other part at the crossings. This is a knot diagram.
One of the most famous knots is not very 'knotty' at all. The unknot is just a circle. A nontrivial knot is any other knot.

The Unknot
The next simplest knot is a trefoil. There are two varieties of trefoils which are mirror images of each other: the left-handed trefoil knot and the right-handed trefoil knot:

Two knots are considered to be equivalent if they can be moved around in space so that they look alike. The following are also diagrams of the trefoil knot.
Questions
How can we determine if two knot diagrams represent the same knot?
Using the knot diagrams we could make the knots out of string, and we could try to arrange them so that they appear the same. If we are lucky, we may succeed and thus conclude they are the same. However, when should we be convinced that they aren't the same? After 10 minutes of trying, an hour of trying, a week of trying?
Exercise
Take two knots made of string and try to determine whether they are the same. Are the left-handed trefoil and right-handed trefoil equivalent?
Crossing Numbers
Distinguishing different knots from knot diagrams can be pretty tricky. Mathematicians have developed invariants which can help distinguish different knots. However, so far there are no invariants which can distinguish all knots. One online source for descriptions of a few simple knot invariants is http://www.cpm.informatics.bangor.ac.uk/exhib/pagesexhib/inv.html>.
The minimum number of crossings that one needs to draw a knot diagram for a particular knot is called the crossing number of the knot. The unknot has crossing number 0 and a left-handed or right-handed trefoil has crossing number 3. There are no knots with crossing number 1 or 2. Can you prove this? There is only one knot with crossing number 4, the figure eight knot .
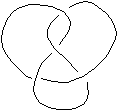
A knot is prime if it can't be formed by cutting two nontrivial knots and then splicing the loose ends together. If a knot is not prime, it is called a composite knot.
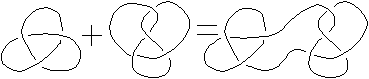
You can find pictures of all the prime knots with 9 or fewer crossings at http://www.atractor.pt/nos/tab-bq-eng.html.
Challenge

Can you make a knot out of your high school? In teams of 3 or 4, take some string and walking the hallways, make a knot. Use the masking tape to occasionally attach the string to the floor (about every 15 or 20 feet). Each group should have different colored masking tape so that you can distinguish your knot from the other teams' knots. Make sure that the string is not in a position to trip someone. If you return to your string, the current strand can not cross under the strand already placed, and you must return to your starting position.
Can you make a nontrivial knot? Draw a diagram of the knot on paper. It's a good idea to try and draw the diagram as you go!
Here are some pictures of students making knots at Ithaca High School!