Back to Graph Theory

Answers to Instant Insanity

  1. How many different ways are there to set up the cubes in a stack? (Note that moving a cube from the top to the bottom which maintaining which colors are on which side results in a stack that is essentially the same since ordering of the colors on the stack does not matter.)

    3(24)3
  2. What seems to be the constraint in getting colors to line up? If you have one side of the tower in all different colors, which colors in the tower can’t you change anymore?

    The colors on the opposite side

  3. Consider a stack that worked:

    You have a stack of blocks with the following alignment of colors:

    Draw two graphs, one for each of the front-back and left-right pairs. For each, the vertices are given labeled by colors. On the front-back graph, draw an edge between two colors if one of the blocks has those colors on the front and back faces. Label edges by the number of the block the pair is from. Draw a similar graph for the left-right pairs.

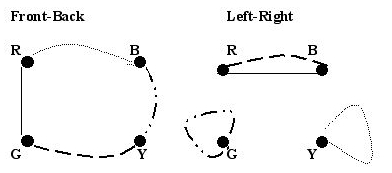
    What do you notice about the graphs? What similarities do they have? Are the similarities enough to guarantee that the stack will work? Why or why not?

    Both graphs have one edge per cube and two edges per color(vertex).

    This will guarantee that the stack will work, since we can follow the edges around and make the first vertex of each edge the front and the second the back (or left and right respectively) so that each side of the stack has all different colors.

    So how can we use what we learned to FIND a solution?

    Above we noted that it is opposite pairs of faces that matter!

    We also noted that if we draw edges on a graph for these pairs, we need to find two subgraphs where:

    1. each color in the subgraph has degree two
    2. there is an edge in each subgraph from each cube

    3. the two subgraphs use a total of eight different edges.

    Try drawing a graph for the set of blocks that you have! For convenience, there are spaces on the paper to put the blocks so you remember which is which.

    Example:

    Now you can put the cubes together to win!

 

Other variations:

  1. What if you have 5 cubes with 5 colors? Can you get a method of solution for such a set?

    The method of solution is very similar…make a graph with opposite faces as edges, but now you have 5 colors, so 5 vertices. You still want to find two subgraphs using 10 total edges, now, where each vertex has degree 2 and there is an edge from each block.
  2. Moshe’s Insanity: You have 8 blocks with 6 different colors of faces. You want to form them into a 2x2x2 cube so that the cube’s faces are 6 different solid colors. Can you use what you learned from Instant Insanity to find a way to win this?

    This is MUCH more complicated. Of course, there are also many more combinations of blocks! The key here is to note the oriented corners of the smaller blocks. These are the parts that will be seen in the larger block and they must be set up so that a whole large block can have these orientations. Most of the possible larger blocks will be ruled out because some of the orientations of their corners do not exist on the smaller blocks. One possible set of blocks with only two (very similar) solutions is: