Rules

You are given four cubes with sides of four different colors:

Find a way to stack the cubes in a tower so that from whichever side you look at the tower, you see all four colors! The goal is to learn a method of solution for this game so you can solve any stack in about 5 minutes!

How to win

1. How many different ways are there to set up the cubes in a stack? (Note that moving a cube from the top to the bottom while maintaining which colors are on which side results in a stack that is essentially the same since ordering of the colors on the stack does not matter.)

   Answer

    

2. What seems to be the constraint in getting colors to line up? If you have one side of the tower in all different colors, which colors in the tower can’t you change anymore?

   Answer

    

3. Consider a stack that worked:

   You have a stack of blocks with the following alignment of colors:

   Block	Left	Front	Right	Back
   1	R	G	B	R
   2	Y	R	Y	B
   3	B	Y	R	G
   4	G	B	G	Y

   Draw two graphs, one for each of the front-back and left-right pairs. For each, the vertices are given labeled by colors. On the front-back graph, draw an edge between two colors if one of the blocks has those colors on the front and back faces. Label edges by the number of the block the pair is from. Draw a similar graph for the left-right pairs.

   

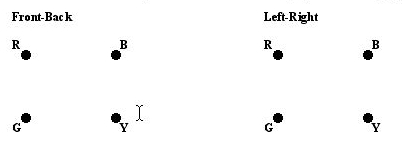
   What do you notice about the graphs? What similarities do they have? Are the similarities enough to guarantee that the stack will work? Why or why not?

   Answer

Finding a Solution

• We noted that it is _______________ pairs of faces that matter!
  
  
• We also noted that if we draw edges on a graph for these pairs, we need to find two subgraphs where:
  
  
  1. each color in the subgraph has degree ______

  2. there is an edge in each subgraph from each __________

  3. the two subgraphs use a total of ___________ different edges.

  Try drawing a graph for the set of blocks that you have! For convenience, you can print out this page and use the spaces below to put the blocks so you remember which is which.

  

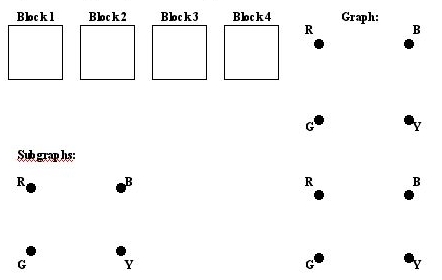
  Now you can put the cubes together to win!

  Answer

1. What if you have 5 cubes with 5 colors? Can you get a method of solution for such a set?

   Answer

2. Moshe’s Insanity: You have 8 blocks with 6 different colors of faces. You want to form them into a 2x2x2 cube so that the cube’s faces are 6 different solid colors. Can you use what you learned from Instant Insanity to find a way to win this?

   Answer

Other Links*

• Play Instant Insanity through your web browser

* These links are for informational purposes only and are from sources outside MEC and Cornell University