Rules

Nim is played starting with piles or rows of objects. Players take turns taking any number of objects from one of the piles. Whoever takes the last of the objects wins!

For example, suppose we start with three piles of M&Ms, the first with 10, the second with 8 and the third with 13:

The first player can choose to take 8 M&Ms from the first pile. However he/she could not take 8 from the first pile and 2 from the second pile, since he/she can choose only from one pile.

You can play online here

Questions

1. How can you win NIM if you play with two piles? Does one of the players have a winning strategy? Which player?

   Hint

   Answer

2. How can you win NIM if you play with two piles? Does one of the players have a winning strategy? Which player?

   Hint

   Answer

3. Can you generalize to have a winning strategy for any number of piles? When is it advantageous to be the first player? Second player?

   Hint

   Answer

Variation: Northcott's Game

Rules

Each of the two players has a different color of counters -- say black and white. A rectangular checkerboard is set up with one of each color counter in each row. Players take turns moving a counter of their color anywhere within its row without jumping the other player's counter. The winner is the last to be able to make a move.

For example, on a 2x7 board, each player has two counters, one in each row. We could start as below:

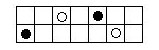
You can play Northcott's game online here.

Questions

1. How are the two games related? How are they different?

   Hint

   Answer

2. What is a winning strategy for winning Northcott's game? When is it advantageous to be the first player? Second player?

   Hint

   Answer

3. What happens if you can move either person's counters?

   Hint

   Answer

4. Can you make up other games like NIM? You can find out about games others made up which are similar to NIM here.