If you started with 3 vertices, there is no way that someone will win (at most a player colors two edges) so the game ends in a draw. Is there always the possibility that the game ends in a draw? Or can you start with some number of vertices and always have a winner?
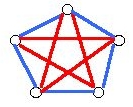
First, notice that a game on five vertices can end without either player having a triangle:

(This does assume that the players are playing randomly and without strategy.)
Now, consider a game played on six vertices, labeled A, B, C, D, E, and F. If the game ends without a winner, all the edges are colored. Then either the first player or the second has colored 3 of the edges from A to the other vertices. Suppose it is the first player, and that he or she colored the edges to B, C and D. In order for the first player not to have colored a triangle, he/she can have colored any of the edges between B, C and D. But then the second player would have a triangle of edges between B, C, and D! The same would happen if the second player had three edges from A or if they were to vertices besides B, C, and D. So any game on six vertices must have a winner.
Since any complete graph with more than six vertices contains a complete graph on six vertices, any game that starts with six or more vertices will have to have a winner.
The idea of looking for the smallest complete graph such that, no matter how the edges are colored, one of the colors has a specific subgraph (such as the triangle above) is called Ramsey theory. In the case of the triangle, since we are trying to draw a complete graph on 3 vertices, we call this number R(3,3). That is, R(3,3) is the smallest number of vertices such that if you color all the edges between the vertices red and blue, there has to be a red complete graph on 3 vertices (a triangle) or a blue complete graph on 3 vertices. So we proved above that R(3,3) = 6. It has been proved that no matter which graph you pick for each player to try to color to win (or even if there are different graphs!) there is some number of vertices which will guarantee there is a winner. However, what this number is not known in most cases!
To find out more about Ramsey theory, consider the following links: