What if you are trying to get a different graph? Say a complete graph on four vertices in your color, or a cycle of four edges?
Ramsey theory has also proved that no matter which graph you pick for each player to try to color to win (or even if there are different graphs for different players!) there is some number of vertices which will guarantee there is a winner. However, what this number is is not known in most cases! We will write R(k,l) for the smallest number of vertices such that if we colored all the edges red and blue, there is either a red complete graph on k vertices or a blue complete graph on l vertices. We will write
Kn for the complete graph on n vertices. (So K3
is a triangle.)
Above we proved that R(3,3)=6. Also note that R(k,1) = R(l,k) because if we can find either a red Kk or a blue Kl no matter how we color the edges, we could just switch all the colors on the edges and have either a red Kl or a blue Kk.
If you needed to win by coloring the edges of a K4, then to guarantee a winner we need at least R(4,4) vertices. Let's try to find an estimate
for R(4,4). If we can find a number of vertices n that guarantees
either a red K4 or a blue K4 then we'll know either R(4,4)=n or R(4,4) < n.
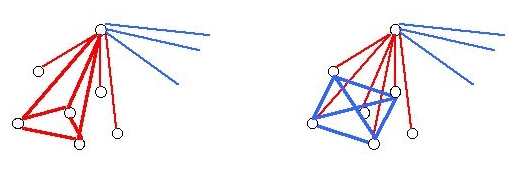
We can build up to a K4 by finding a triangle in one color and another vertex such that all the edges to the triangle are the same color.
So start at a vertex,v the way we did to find R(3,3). Call the set of vertices which have red edges from v S. Suppose S is big enough that we can guarantee that there is a triangle in red, as in the figure to the left,
or that there is a blue
K4, as in the figure to the right.
Then we have either a red K4 or a blue K4!
So we want to have at least R(3,4) red edges (so S has R(3,4) vertices),
guaranteeing either a red K3 or a blue K4. Note that K4 is shown in
thick lines.

But what if we don't have enough red edges for this to happen? Then we want there to be enough blue edges so that there is either a red K4 or a blue K3. This is just the same as the last question, except with colors switched! So if we don't have R(3,4) red edges, we need R(4,3)=R(3,4) blue edges! If there are 2R(3,4) - 1 edges from v, then there must be either R(3,4) red edges or R(3,4) blue edges by the pigeon hole principle. So if we have 2R(3,4) vertices, then we know we have a winner in the game when each player is trying to make a K4. (We showed either R(4,4)=2R(3,4) or R(4,4) < 2R(3,4) )
But what is R(3,4)? It turns out that R(3,4)=9. We can get this by an argument similar to that above:
Start with a vertex v and let S be the set of vertices which have a blue edge from v. If S is big enough to have either a red K3 or a blue K3, then all together we get a red K3 or a blue K4 - just what we want! But we know that R(3,3) = 6, so if there are 6 blue edges from v, we get what we want. But what if there aren't 6 blue edges? If T is the set of vertices which have a red edge from v, then we need T to have either a red edge (a K2) or a blue K4. Well, if we have 4 vertices, then we know there is either a red edge or all the edges are blue - a blue K4. This says that R(2,4) = 4, and therefore if there are 4 red edges from v, we are fine. In order to guarantee 6 blue edges or 4 red edges, we need a total of 9 edges. (You can't make 9 edges with at most 5 blue edges and 3 red edges!) So we now know that either R(3,4)=10 or R(3,4) < 10.
But in fact, R(3,4) = 9! The key to noting that we can use the same argument on 9 vertices is by looking at the number of edges of each color to the vertices. By the argument above, in order to avoid a red K3 or a blue K4, we need to have 5 blue and 3 red edges at each of the 9 vertices. But each edge gets counted from 2 ends, so the number of times we count a blue edge should be even. But if each vertex has 5 blue edges, then we count blue edges a total of 45 times - this is a contradiction. Therefore, there is some vertex in a K9 which has either 6 blue edges or 4 red edges and we are done! This shows either R(3,4)=9 or R(3,4) < 9.
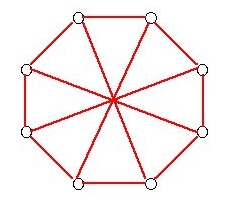
Note that this isn't enough to show that R(3,4) = 9. To show that, we need to show that there is some way to color K8 such that there is no red K3 or blue K4. (Then R(3,4) > 8, so with R(3,4)=9 or R(3,4) < 9, we get R(3,4) = 9 since it must be an integer.) The following graph shows all the red edges of a coloring of K8, and there is no triangle. There is also no blue K4 in all the edges that are not shown. This shows that R(3,4) > 8.
Now, let's put the pieces together! R(3,4)=9 and we know that R(4,4)=2R(3,4) or R(4,4) < 2R(3,4) = 18. In fact, it can be proved that R(4,4) = 18. (Can you find a coloring of K17 such that there is no red K4 and no blue K4?) So if we have at least 18 vertices, then there must be a winner.
Amazingly, no one knows R(5,5)! We just know that 43 < R(5,5) < 49. Paul Erdos told this story: "Aliens invade the earth and threaten to obliterate it in a year's time unless human beings can find [R(5,5)]. We could marshal the world's best minds and fastest computers, and within a year we could probably calculate the value If the aliens demanded [R(6,6)], however, we would have no choice but to launch a preemptive attack" (Graham, R.L. and Spencer, J.H. Ramsey Theory, Scientific American July 1990: 112-117).
If you are playing that you need a cycle of 4 edges to win, 6 vertices still works to guarantee a winner. Can you figure out why?