If no one won after placing the counters, can the players always slide a counter until someone wins?

The empty space can be one of three positions up to symmetry: a corner, the center, or a middle of the side of the square.

1. The empty space is at a corner (shown in white). If the next player can't move, the last player must have all the places around the corner which could move to the corner, shown in blue below. The next player must have four of the yellow spots -- but this means that the next player already has a 3-in-a-row.
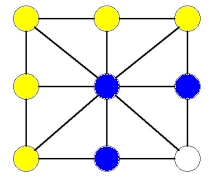
2. The empty space is at the center. Since every other spot can move to the middle, the next player can always move.
3. The empty space is on the side of a square (shown in white). Then, if the next player can't move, the last player has the blue places:

   Since they are sliding, there is no 3-in-a-row yet, so the next player has the red spaces. The last player must have the yellow space between the two reds.

   This gives the final placement:

   

   This position could not occur after one of the players slid a counter, since then the blue player must have slid a counter out of this open place, so he/she must have had a 3-in-a-row before the move.

   However, in order for the position above to occur immediately following the original play, the blue player must have had an opportunity to win in the last move and did not. The blue player had the last move and could have chosen the open place along the edge, which would have completed a 3-in-a-row, either horizontally or vertically (depending of where he/she had played previous counters).

Since the players can always slide a counter, someone will win. If whoever is in the middle stays there, all the sliding counters will move in a circle around the center. When we consider the 7 counters around the outside (and one empty space), either the player with his/her counter in the middle will have two counters which are separated by exactly two of the other player's counters and will eventually win (why?) or one of the players has three counters in a row and will win when these are all along one side. These are the only possibilities since if the player with the counter in the center does not have two counters separated by two of the other player's two of this player's counters must be next to each other and the other player must have at least 3 counters in a row.