Not only does the first player have an advantage, as mentioned in question 2, but no matter what the second player does, they will always be able to win if they play correctly -- that is, the first player has a winning strategy.

Since the middle space is so important, the first player's first move should be to take this space. Then the second player has a choice: to take a space along a side, or a corner. Let the first player be red and the second blue.

Suppose the blue player takes a space along the side. Then the red player can win, even without having to slide any pieces! The red player can respond by taking a corner next to the blue player's space:

Then the blue player is forced to block the red player:

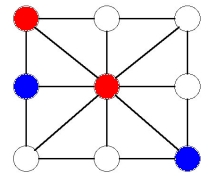
Now the red player can play in the corner, as below, so that he has two possible moves to get 3-in-a-row. Now, no matter which one the blue player blocks, the red player can win.

Can you find any other ways to win if the blue player goes along an edge?

Suppose the blue player plays in a corner. Then the first player can play in an adjacent corner to the one the blue player played in. Now the players take turns blocking the other, as shown in the following sequence of moves:

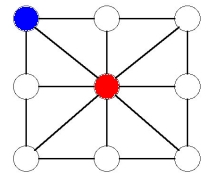
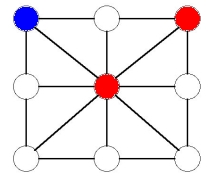
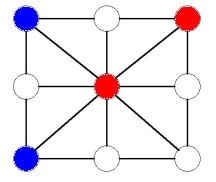
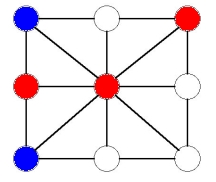
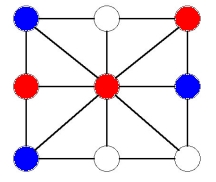
Now the red player can choose to play either in the bottom middle or bottom right. If he plays in the bottom middle, the blue player is forced to play in the top middle or else the red player will win immediately by sliding a counter. This gives:

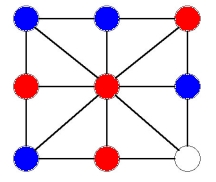
Now the red player wants to maintain his position in the center, so he/she slides the red counter in the bottom middle to the bottom right. The blue player must move his blue counter from the bottom left to the bottom middle and finally the red player moves the counter along the left side to the bottom left and wins. This sequence of moves is shown below:

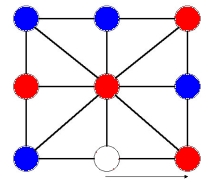
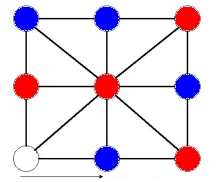
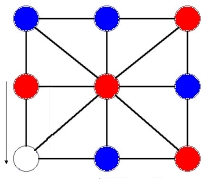
Notice that the counters along the outside of the square never change order in the sliding process as long as the red player does not move his/her counter out of the middle. Therefore, the blue player could never win even if they kept sliding the counters since he doesn't have 3 blue counters in a row along the outside. Even if we don't get to this exact position for starting to slide, as long as none of the 3 red counters not at the center are next to each other, the red player will be able to win sometime in the sliding. This is because at least two of the red counters must have at least two blue between them and these two will end up opposite when the two blues and the open space are between them.