 and
and
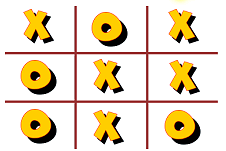
Can the game end in a draw?
No. The game cannot end in a draw. Suppose it did.
Then each of the boards on each level must end in a draw.
There are basically two ways (up to symmetries and switching X's and O's)
for a normal game of Tic-Tac-Toe to end in a draw:
 and
and
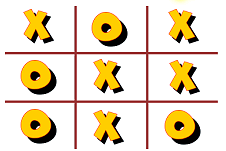
Now consider a 3D game with each of these as the bottom board. Working with the left board first, consider the center space in the middle board. It must be either an X or an O. If it is an O, the middle row on the top board must have Xs on the left and right in order to avoid 3-in-a-rows between the three levels. Similarly, there must be Xs in the middle of the bottom row and on the left and right in the top row of the top level.

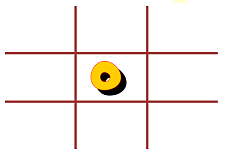
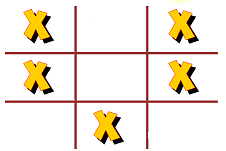
Then all the other spaces on the top level must be Os in order to block 3-in-a-rows on the top level:



Then the bottom corners of the middle board must be Xs in order to block vertical 3-in-a-rows. Also the bottom middle of the middle board must be an X to block diagonal 3-in-a-rows between the levels. But this forces there to be 3 Xs in a row! So we can't get a draw this way:

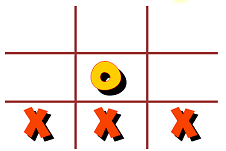

Now consider the possibility where we start with the same bottom level and the center square of the middle level is an X. Then we are forced to have 4 Os in the top level: the center, top center, and bottom corners.


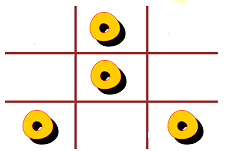
Then we are forced to have Xs in the top level top corners, and bottom middle. Also we must have Xs in the middle level in the top, middle and bottom corners.
But now there are 3 Xs in a row, shown in red: a top corner on the bottom level, the middle top on the middle level, and the opposite top corner on the top level.


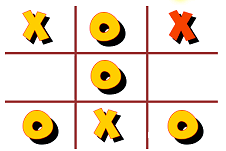
Similarly, if we start with the other base and have an O in the center of the middle board, we are forced to the following positions:
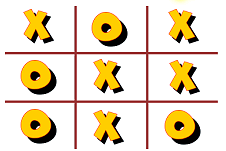


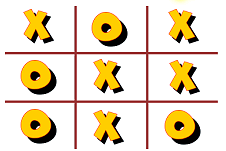
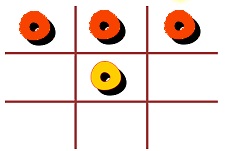

If instead, we have an X in the center of the middle board, the following moves are forced:
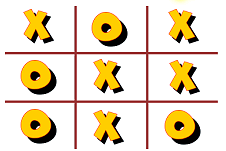

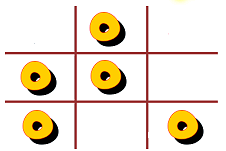
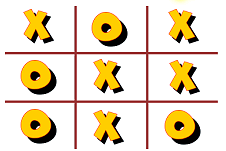


Therefore, there is no way for the game to end in a draw.