Game Theory
VII. Solutions\Hints to Problem Sets
Solutions/Hints to Problem Set 1 :
Step 1: Eliminate R, by noticing that no matter what strategy P1 takes, it is never best for
P2 to choose R.
Step 2: Eliminate M, by noticing that no matter what strategy P2 takes, it is never best for
P2 to choose M.
Step 3: Eliminate L, by noticing that no matter what strategy P1 takes, it is never best for
P2 to choose L.
Step 4: Eliminate T, by noticing that no matter what strategy P2 takes, it is never best for
P2 to choose T.
Giving you the solution of (B,C).
Or, equivalently you could use the arrow method to get the solution.
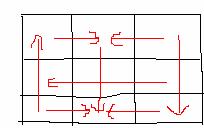
The way we create this diagram is by supposing (for example) P2 chooses L, then draw an arrow depicting which choice P1 prefers. In total fix one player’s strategy then draw an arrow depicting the preference of the other. Do this for each possible strategy for each possible player.
The way we find the Nash Equilibrium from this diagram is to look at where (if we follow the arrows in succession) all arrow point to. It is not necessarily true that every game represented this way will have a NE.
Notice that this way gives the exact same solution as before.
Question? Does every game have a unique Nash Equilibrium?
Answer: NO!
Consider the game entitled
|
Strategy |
Opera |
Bullfight |
|
Opera |
(1,2) |
(0,0) |
|
Bullfight |
(0,0) |
(2,1) |
Now we try to find this games NE, using the arrows method giving us

Hence, for this game we have two Nash Equilibria (one can check that the arrow method give the NE of the game by referring to the definition of NE and that if there are no NE then the arrow method never lead to the “sink points”).
Question? Does every matrix game (the games we have been talking about) have a Nash Equilibrium?
Answer: No!
Consider the game, with solution
|
Strategy |
L |
R |
|
T |
(0,3) |
(3,0) |
|
B |
(2,1) |
(1,2) |

This results in this game having no NE.
End of Solutions/Hints to
Problem Set 1
Solutions/Hints to Problem Set 2 :
The Saddle Point is where the payoff is -3.
End of Solutions/Hints to
Problem Set 2
Solutions/Hints to Problem Set 3 :
Consider again the game, with solution (recall that it has no NE). Find the Nash Equilibrium in Mixed Strategies.
|
Strategy |
L |
R |
|
T |
(0,3) |
(3,0) |
|
B |
(2,1) |
(1,2) |

If done properly you will find that p1=1/4 and q1=1/2.
End of Solutions/Hints to
Problem Set 3
Solutions/Hints to Problem Set 4 :
This is a simple “critical value problem”.
End of Solutions/Hints to
Problem Set 4
Solutions/Hints to Problem Set 5 :
Neg. set on line segment (2,4)
and (4,2), N=(x,y) which maximizes (x-2)(y-1)
equation of the line is y= 6-x (2<=x<=4) . We must maximize (x-2)(6-x-1)
on (2<=x<=4), doing so gives us a max at x=7/2 and y=5/2 and we get this
by playing 5/6C+1/6D which will be our solution.
End of Solutions/Hints to
Problem Set 5
Solutions/Hints to Problem Set 6 :
The manufacturer can minimize cost per unit with the route A to B1 to C1 to D, for a total cost per unit of 14.
End of Solutions/Hints to
Problem Set 6
Solutions/Hints to Problem Set 7 :
On the branch (P2 to P3), P3 will choose their highest payoff of 5.
On the branch (P2 to P1), P1 will choose their highest payoff of 2.
On the branch (P2 to P1 to P2), P2 will choose their highest payoff of 4.
On the branch (P2 to P1 to P3), P3 will choose their highest payoff of 3.
Now knowing this if P2 were to give P1 the option between (P2 to P1 to P2) and (P2 to P1 to P3), P1 would choose (P2 to P1 to P3), since it maximizes their payoff at 2.
Knowing these facts P2 can choose between a payoff of 3,1,or 2. So they choose to go with P3 to maximize their payoff.
End of Solutions/Hints to
Problem Set 7