Game Theory

 

 

 

 

IV. Games with Cooperation

 

 

 

Example: How should the following game be played cooperatively

Strategy

A

B

A

(2,6)

(10,5)

B

(4,8)

(0,0)

With the arrow method

Should they pick the strategy with the highest total payoff and split it? To do this they would play (A,B) with payoffs (5,10) giving each player 7.5. They should not do this because P2 could play non-cooperatively and get a payoff of 8.

 

So any reasonable solution to a cooperative game should be

1)      Pareto optimal (no other outcome better for both players)

2)      At or above what both players could receive through non-cooperative play

 

Now through mixed strategies any point inside the diagram could be achieve (with expectations).

 

 

You could check and see that through mixed strategies the MSNE is (10/3, 6) and that promises and threats won’t help this game.

 

How can we choose (in the negotiation set) a single outcome as fairest. Negotiate above some the (Status Quote), if negotiations fail then take the status quote point.

 

Arbitration Scheme. – Method of solution

 

Any reasonable Arbitration scheme must satisfy.

 

Axiom 1: Rationality; solution point must be in the Negotiating Set.

 

Axiom 2: Linear Invariance; If either Scott’s or Peter’s utilities are transformed by a positive linear function the solution should be transformed by that same function.

“This guarantees that a bargaining solution will not be affected by changing the scale or units in which utility is measured.” <Ali,193>

 

Axiom 3: Symmetry; if the polygon happens to be symmetric about the line with slope +1, the solution point should lye on this line “non-discrimination”

 

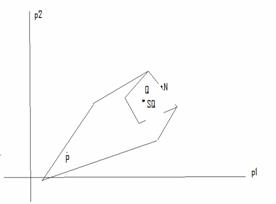
Axiom 4: Independence of Irrelevant Alternative: suppose N is a solution point for P and Q C P w/ SQ, N in Q the N is a solution for Q also.

 

Theorem [Nash, 1950] there is only one Arbitration solution which satisfies Axiom 1 to 4: It is If SQ: = (Xo, Yo), the arbitrated solution point N is the point (x,y) in P w/ X>=Xo Y >=Yo that maximizes (X-Xo)(Y-Yo)

 

            Note: If the max of (X-Xo)(Y-Yo) is 0, then say (Y-Yo) is always negative then the unique solution is max {X ≥ Xo 1 X in P }.

 

 

Problem Set 5 : Rose & Colin must agree on the 4 outcomes A = (0,0) B = (2,0) C = (4,2) D = (1,5) or some fixed probability between them with  SQ = (2,1). How would a Nash Arbitrator propose a fair solution? 

 

End of Problem Set 5

 

 

 

 

 

 

 

References and Further Reading:

1.C. D. Aliprantis, and S. K. Chakrabarti, Games and Decision Making, Oxford   

   University Press, New York, 2000.

2. P. Straffin, Game Theory and Strategy, The Mathematical Association of America, DC,

   1993.